| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- back propagation
- 세그먼트 트리
- object detection
- 가끔은 말로
- 다익스트라
- DP
- 우선 순위 큐
- 미래는_현재와_과거로
- dfs
- 플로이드 와샬
- NEXT
- 알고리즘
- 2023
- 가끔은_말로
- 백트래킹
- 문자열
- dropout
- Overfitting
- 회고록
- 자바스크립트
- tensorflow
- 조합론
- 이분 탐색
- lazy propagation
- BFS
- pytorch
- 크루스칼
- 분할 정복
- c++
- 너비 우선 탐색
- Today
- Total
Doby's Lab
Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift 본문
Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
도비(Doby) 2023. 1. 22. 13:18✅ Contents
- Intro
- Abstract
- 1. Introduction
- 2. Towards Reducing Internal Covariate Shift
- 3. Normalization via Mini-Batch Statistics
- 4. Experiments & 5. Conclusion (skip)
- Outro
- Reference
✅ Intro
📄 Motivation
Batch Normalization에 대해 알게 된 후, 남아있는 궁금점을 해결하기 위해서는 직접 원문을 보아야겠다는 생각이 들었습니다.
궁금했던 것으로는 BN(X)와 Activation의 선후 관계나 네트워크마다 Batch Normalization의 방법이 다른 것들이 궁금하기도 했고,
'Internal Covariate Shift를 해결하는 것이 아닌 다른 것을 해결한다'는 추후에 나온 다른 논문에서 했던 얘기였지만 조금 근 본에 대해 다루어서 궁금증을 해결해보고 싶었습니다.
Batch Normalization에 대한 개념을 다룬 포스팅 (기초적인 내용)
https://draw-code-boy.tistory.com/504
Batch Normalization이란? (Basic)
Batch Normalization Batch Normalization는 모델이 복잡할 때, 정확히는 Layer가 깊어지면서 가지는 복잡도가 높을 때 일어나는 Overfitting을 해결하기 위한 기법입니다. Batch Normalization이 어떻게 작동되는지
draw-code-boy.tistory.com
📄 Paper Link
https://arxiv.org/abs/1502.03167
Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
Training Deep Neural Networks is complicated by the fact that the distribution of each layer's inputs changes during training, as the parameters of the previous layers change. This slows down the training by requiring lower learning rates and careful param
arxiv.org
✅ Abstract
DNN 구조의 Network를 학습시키는 것은 이전 layer에서 Parameter가 달라짐에 따라 각 layer의 input의 Distribution이 달라져서 학습시키기 어렵습니다.
이러한 현상은 낮은 Learning Rate, 조심스러운 Parameter Initialization을 요구하고, Distribution이 달라짐에 따라서 non-linearity(= Activation)에서의 saturation(Activation의 편미분이 0이 되어 업데이트가 없어지는 현상)에 따라 가중치 업데이트가 중단되는 사태까지 발생할 수 있습니다.
논문에서는 이러한 현상을 'Internal Covariate Shift'라고 합니다.
이러한 문제를 대응하기 위해 논문에서는 각 mini-batch에 따른 Normalization을 진행하고, 이를 모델의 한 부분으로 적용을 시켜 문제를 해결하는 방법을 제안합니다.
제시된 방법을 통해 더 높은 Learning Rate를 사용할 수 있도록 하고, Initialization에 대해 조금 덜 주의해도 되고, Regularization의 역할까지 하여 Dropout의 의존성을 줄이도록 합니다.
✅ 1. Introduction
📄 Domain Adaptation
Introduction에서는 SGD에 대한 설명과 mini-batch의 이점에 대해 말하며 시작합니다.
그리고, 각 layers의 input에서 분포의 변화는 각 layer로 하여금 새로운 분포에 지속적으로 적응해야 한다는 문제를 삼고 있습니다. (Domain Adaptation)
그러나, Covariate Shift는 하위의 sub-network나 layer에도 적응되기 위해서 Learning System 전체를 넘어 확장될 수가 있습니다.
왜 그런지에 대해서 한 network를 예로 들어 설명합니다.
$$ l = F_2(F_1(u, \theta_{1}), \theta_{2}) $$
수식에 대해 설명하면, 아래와 같은 구조입니다.
$$ F(input, parameter) $$
또한, \(F_2(F_1(u, \theta_{1}), \theta_{2})\)는\(x=F_1(u, \theta_{1})\)로 표현한다면, \(F_2(x, \theta_{2})\)로 간단하게 나타낼 수 있습니다.
이에 따른 \(\theta_{2}\)의 mini-batch Gradient Descent의 과정은 아래와 같이 나타날 수 있습니다.
$$ \theta_2 = \theta_2 - \alpha\frac{1}{m}\sum_{i=1}^{m}
\frac{\partial F_2(x_i, \theta_2)}{\partial \theta_2} $$
이러한 구조는 \(F_2\)라는 단일 네트워크에 \(x\)라는 input이 들어가는 것과 같습니다.
그러므로, training data나 test data가 모두 같은 분포를 가지는 것이 효율적이라는 말을 하고 있습니다.
input data의 분포를 시간이 지남에 따라 고정함으로써 \(\theta_2\)가 계속 변화되는 분포에 따라 새롭게 적응할 필요가 없기 때문입니다.
📄 Gradient Vanishing & Saturation
또한, sub-network에 대한 input의 고정된 분포는 sub-network의 외부 layer들에도 긍정적인 효과를 초래할 것이라는 말을 합니다.
layer를 통해 출력한 output(\(Wu + b\))을 시그모이드의 입력 값이라고 가정하였을 때, 이 값의 크기가 커짐에 따라 Gradient Vanishing이 발생합니다. 이에 따라, 학습의 속도가 느려지는 것은 물론입니다.
또한, 시그모이드에 대한 입력값은 W, b의 영향과 그 아래의 layer의 모든 parameter들의 영향을 받기 때문에 Back-Propagation의 과정에서 Vanishing 뿐만 아니라 Saturation 현상까지 나타날 수 있습니다.
(이에 대해 해결하기 위해 sigmoid보다는 ReLU activation을 추천합니다.)
그래서, nonlinearity(= activation)에 대한 input의 distribution이 안정성을 갖춘다면, Vanishing이나 Saturation의 문제에 Gradient Descent가 덜 방치될 수 있고, 학습을 더 가속시킬 수 있습니다.
📄 Suggest 'Batch Normalization'
layer를 거침에 따라 분포가 변하는 현상을 'Internal Covariate Shift'라고 언급합니다.
이에 따라 제시한 방안이 'Batch Normalization'입니다.
각 input(mini-batch)의 평균과 분산을 통해 Normalization을 함으로써 얻는 이점들은 아래와 같습니다.
- Accelerated Training using much higher learning rates (= 높은 학습률을 적용할 수 있음으로써 가속화된 학습)
- Gradient flow through the network, by reducing the dependence of gradients on the scale of parameters or of their initial values (= 파라미터와 초깃값의 스케일에 따른 gradient의 의존성을 줄임)
- Regularizes the model and reduces the need for Dropout (= 규제를 함으로써 Dropout의 필요성을 줄임)
✅ 2. Towards Reducing Internal Covariate Shift
📄 Whitening
그래서 Fixed Distribution을 위해 Whitening 기법을 사용해 봅니다.
Whitening이란 평균을 0, 분산을 1로 만들고, 모든 데이터를 decorrelated 하게 만드는 방법입니다.
- 이 과정에서 Covariance Matrix와 Inverse를 사용하여 계산량이 엄청 많아집니다.
- 또한, 이 과정에서 선형대수학이 쓰여 선형대수학을 공부해야겠다는 계기가 되었습니다.
하지만, Whitening은 Optimization(= Gradient Descent)의 과정과 별개로 이루어지기 때문에 Gradient Descent의 과정에서 Whitening에 대한 업데이트도 되어야 하는데 그러질 못 해서 Gradient Descent의 효과를 감소시킵니다.
예를 들어, 한 layer에 대한 input을 \(u\)라고 두고, 학습을 통해 만들어진 bias를 \(b\)라고 하고,
이로 인해 \(x=u+b\)라는 결과가 만들어진다고 가정해 봅시다.
전체 데이터의 평균을 뺌으로써 normalize를 합니다.
$$ \hat{x} = x - E[x] $$
(\(x=u+b, \chi = \{x_{1...N}\}\) set of values of x over the training set, \(E[x] = \frac{1}{N}\sum_{i=1}^{N}x_i\))
Gradient Descent에 따라 \(b = b + \Delta b\)로 업데이트될 것입니다.
(\(\Delta b = -\alpha\frac{\partial l}{\partial \hat{x}}\))
그럼 업데이트 과정에서 아래와 같은 일이 발생합니다.
$$ u + (b + \Delta b) - E[u + (b + \Delta b)] = u + b - E[u + b] $$
이 과정에 따라 b의 영향은 사라지고, Loss에서는 변함이 없게 됩니다.
하지만, Back-Propagation은 계속 진행되니 \(b\)만 무기한으로 커지게 됩니다.
이러한 문제는 단순히 E[x]만 빼는 것이 아니라 표준편차로 나누어주거나 scaling의 과정까지 포함될 경우 더욱 모델이 악화되는 경향이 있다고 합니다.
결론적으로, Normalization이 Gradient descent Optimization의 과정에 필수적으로 포함되어야 합니다.
그렇게 함으로써, 모델의 Parameter들이 Normalization을 설명할 수 있어야 합니다.
📄 Whitening Back-Propagation
그래서, \(x\)를 input vector라고 해봅시다. 그리고, \(\chi\)는 전체 데이터셋입니다.
Normalize 한 값은 아래와 같습니다.
$$ \hat{x} = Norm(x,\chi)$$
이렇게 되었을 때, Back-Propagation의 관점에서 보면
$$ \frac{\partial Norm(x,\chi)}{\partial x}, \frac{\partial Norm(x,\chi)}{\partial \chi} $$
위 derivative들을 계산해야 합니다. 이 과정에서 Jacobian, Covariance Matrix, inverse 등의 개념이 나오는데 아직 선형대수학에 관해 잘 모르기 때문에 계산량이 엄청 많다는 것만 알고 넘어가겠습니다.
즉, 계산량이 엄청 많다는 것 때문에 대체적인 방법이 필요합니다.
대체적인 방법에 대한 요구 사항으로는 미분이 가능한 Normalization 방법이어야 하고,
parameter를 업데이트할 때, 전체 데이터셋에 대한 분석이 필요로 없었으면 하는 것입니다.
이전의 방법 중 하나는 단일 sample에 대한 계산된 통계를 이용하거나, Image Network의 경우에는 특정한 주어진 위치의 feature map을 이용해 계산하도록 했는데, 이러한 것은 네트워크의 정보에 대해 손실이 우려되는 방법입니다.
그래서, 전체적인 데이터셋이 필요하지만 데이터셋에 대한 계산량이 많기 때문에 whitening을 대체할 방법이 필요한 것입니다.
✅ 3. Normalization via Mini-Batch Statistics
whitening이 계산량도 많고, 모든 곳에서 미분 가능이지는 않기 때문에 2가지를 Simplification(간단화) 해야 합니다.
📄 Simplification (1): Normalize each scalar feature independently
각 dimension 별로 scalar 값들의 Normalization을 진행하자는 것입니다.
이러한 Normalization의 기법은 decorrelated 하지 않은 경우에도 수렴을 가속화시킵니다.
예를 들어, \(x\)라는 input vector가 d-dimension을 가지고 있다면, \(x = (x^{(1)}...x^{(d)})\)로 보아서 아래와 같이 Normalize 한다는 뜻입니다.
$$ \hat{x}^{(k)} = \frac{x^{(k)} - E[x^{(k)}]}{\sqrt{Var[x^{(k)}]}} $$
그리고, 간단하게 Normalize만 해서는 안 됩니다.
예를 들어, sigmoid 함수로 Normalized 된 값들을 이용하면 sigmoid의 Non-linearity가 보장되지 않기 때문입니다.
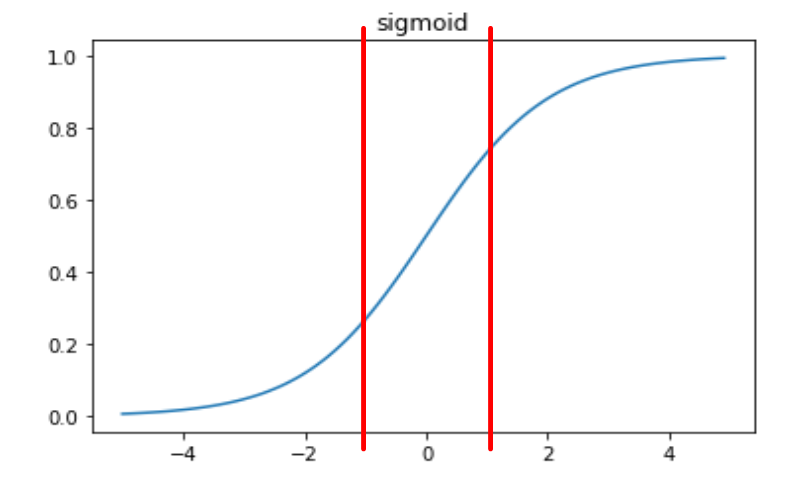
무슨 소리냐면 Gaussian Normal Distribution에 따르면 정규화된 값들의 99.7%는 \([m-3\sigma, m+3\sigma]\)에 속한다고 알려져 있습니다. 정규화된 값들을 모두 sigmoid를 통해 통과시키면 sigmoid의 Non-linearity를 잃게 된다는 뜻입니다.
그러면서 논문에서는 이 말을 강조합니다.
\(the\;transformation\;inserted\;in\;the\;network\;can\;represent\;the\;identity\;transform.\)
transformation을 Network에 적용할 때, 의도적인 변환을 줄 뿐, 다른 변환을 주지 말라는 뜻으로 다가와서 적어두었습니다.
변환이 identity 하게(=항등 하게) 이루어져야 한다는 말입니다.
그래서, 어떻게 Non-linearity를 보장시킬 건지에 대한 것은 Normalize 된 값에 parameter를 추가합니다.
$$ y^{(k)} = \gamma^{(k)}\hat{x}^{(k)} + \beta^{(k)} $$
\(\gamma^{(k)}\)는 초기 값이 \(\sqrt{Var[x^{(k)}]}\)로 세팅되고, \(\beta^{(k)}\)는 \(E[x^{(k)}]\)로 세팅이 되어 학습을 통해 최적의 Parameter를 찾아갑니다.
📄 Simplification (2): mini-batches in stochastic gradient training
각 mini-batch의 평균과 분산을 구하여 Gradient descent를 진행할 수 있도록 하자는 것입니다.
mini-batch \(B\)의 사이즈를 \(m\)이라고 고려하고, \(x^{(k)}\)는 편의성을 위해 \(k\)를 생략하면, 아래와 같은 mini-batch가 만들어집니다.
$$ B = \{x_{1...m}\} $$
그리고, normalized 된 값들 \(\hat{x}_{1...m}\)을 \(\gamma\)와 \(\beta\)에 의한 선형적인 변환을 거치면 Batch Normalization이 되는 것입니다.
$$ BN_{\gamma, \beta} : x_{1...m} \rightarrow y_{1...m} $$
결과적으로 Batch Normalizaing Transform에 대해 정리하면 아래와 같습니다.
\(\epsilon\)이라는 상수 값을 더해주는 이유는 분산이 0이 되는 경우를 고려하여 수치적 안정성을 위해 넣어준다고 합니다.

\(\gamma\)와 \(\beta\)가 학습을 통해 optimal 한 값을 찾아갈 때, 아무런 곳에도 의존적이지 않을 거란 생각을 하면 안 됩니다.
오히려 \(BN_{\gamma, \beta}(x)\)는 많은 샘플들에게 많이 의존하기 때문입니다.
그리고, Batch Normalization의 parameter들은 Back-Propagation의 과정에서 Gradient Descent를 통해 학습할 수 있어야 합니다.

미분의 연쇄 법칙에 의해 아래와 같이 정리 가능하며, 미분이 가능합니다.
이에 따라 Batch Normalization layer를 통과함으로써, Internal Covariate Shift를 줄이는 분포를 갖는 값들을 다음 sub-network로 넘길 수 있게 되어 학습을 accelerate 시킬 수 있게 됩니다.
더 나아가, Non-Linearity를 보장하여 Identity Transform(항등 변환, 별다른 손실이 없도록)이 되도록 하기 때문에 네트워크의 능력을 보존합니다.
📄 3.1 Training and Inference with Batch-Normalized Networks
Training이 어떻게 되는지 알았으나 Inference가 진행될 때는 어딘가 부족한 점이 보입니다.
Inference 단계에서 '평균', '분산'은 어떤 것을 사용해야 하는가?
논문에서는 크게 2가지 방식을 제안합니다. 2가지 방식 다 훈련 세트의 평균과 분산을 사용합니다.
Population statistics
$$ \begin{align}
E[x^{(k)}] &= E_{B}[\mu_{B}^{(k)}] \\ \\
Var[x] &= \frac{m}{m-1}\cdot E_{B}[\sigma_{B}^{2}]
\end{align} $$
Moving Average
$$ \frac{P_M+P_{M-1}+\cdot\cdot\cdot+P_{M-(n-1)}}{n} = \frac{1}{n}\sum_{i=0}^{n-1}P_{M-i} $$
Population statistics는 비효율적이라 보통 Moving Average의 방식을 사용한다고 합니다.
Inference도 마찬가지로 \(\gamma\)와 \(\beta\)를 사용하여 Scaling과 Shift를 합니다.

📄 3.2 Batch-Normalized Convolutional Networks
Covolution layer에서 \(Wx+b\) 형태로 Batch Normalization을 하는데, 이 때는 \(\beta\)가 shift의 역할을 하면서 \(b\)의 역할을 대체하기 때문에 \(b\)를 없앱니다.
그리고, CNN의 성질을 유지시키기 위해서는 각 Channel을 기준으로 Batch Normalization에 대한 변수가 있어야 합니다.
Convolution을 적용한 Feature Map의 크기가 p x q라고 하고, Mini-batch의 사이즈가 m이라고 한다면,
Channel 별로 m x p x q에 대한 Mean과 Variance를 구하는 것입니다.
그래서 Channel이 n개 라면, 총 n개의 Batch Normalization Parameter(\(\gamma, \beta\))가 생기게 됩니다.
결과적으로, \(\gamma\)와 \(\beta\)는 Channel별로 존재하여 CNN의 성질을 살립니다.
📄 3.3 Batch Normalization enables higher learning rates
Batch Normalization을 함으로써 parameter의 작은 변화가 크게 변동 사항을 가져오지 않게 됨으로써, 더 높은 Learning rate를 가능하게 하였습니다.
또한, Non-linearity의 상실에 대한 문제를 예방함으로써 Saturated Regime 같은 위험성도 줄였습니다.
📄 3.4 Batch Normalization regularizes the model
Batch Normalization이 Regularization의 역할을 하면서 Overfitting을 줄이기 위한 Dropout을 없애거나 줄여도 된다고 합니다.
✅ 4. Experiments & 5. Conclusion (skip)
결국 Batch Normalization이 좋은 결과를 낳는다는 얘기로 생략하겠습니다.
✅ Outro
궁금증을 해결하기 위해 논문을 읽다가 Batch Normalization을 적용함에 따라 얻는 이점들도 공부하게 되면서 기존 프로젝트(Cat & Dog Classification Version 2)에서 디벨롭시킬 부분들이 보였습니다.
아래와 같은 부분들을 적용하여 Version 2.1을 만들어볼 생각입니다.
- Regularization의 역할을 하기 때문에 Dropout의 필요성을 줄임.
- 3. Normalization via Mini-Batch Statistics에서 Non-linearity에 대한 방안을 다루는 것을 보아 BN(X) -> Activation의 구조로 쓰이는 것으로 보임.
그리고, Batch Normalization에 대한 후속 논문 'How Does Batch Normalization Help Optimization'도 언젠가 기회가 된다면 읽어 봐야 할 거 같습니다. Intenal Covariate Shift가 어떻게 제거되었는지 설명이 부족하여 실험을 통해 BN이 성능이 좋은 이유에 대해 설명합니다.
또한, 2023년의 계획이었던 선형대수학, 통계학, 미적분학에 대해 계획을 세우면서도 '아직 내가 필요할까'라는 거리낌에 대한 생각이 있었지만, 처음으로 원론적인 이야기를 다루어보면서 '당장 필요하구나'를 깨달은 공부였습니다.
올해 계획에 확실히 거리낌 없이 진행해야 할 부분들이라는 확신이 들었었습니다.
추가적으로, 영어에 대한 공부도 정말 많이 필요하구나를 느꼈습니다. 모르는 단어만 알아내면 해석이 매끄러울 거란 생각을 했었는데 문맥상 무슨 얘기를 하는 건가 싶어서 해석본을 많이 찾아보아야 했습니다. 물론, 수학적 지식이 없다는 것도 해석에 대해 한몫했습니다.
마지막으로, 다음 논문 리뷰부터는 조금 더 간략화하여 작성해 볼 생각입니다. 조금 더 필요한 필수적인 정보들을 제공하여 불필요한 시간과 글을 줄여서 더 효율적으로 글을 작성해 보겠습니다 :)
✅ Reference
https://dive-into-ds.tistory.com/19
Whitening transformation
Whitening transformation(혹은 sphering transformation)은 random variable의 벡터(covariance matrix를 알고 있는)를 covariance matric가 identity matrix인 variable들로 변형하는 linear transformation이다. 즉, 모든 변수가 uncorrelated
dive-into-ds.tistory.com
https://eehoeskrap.tistory.com/430
[Deep Learning] Batch Normalization (배치 정규화)
사람은 역시 기본에 충실해야 하므로 ... 딥러닝의 기본중 기본인 배치 정규화(Batch Normalization)에 대해서 정리하고자 한다. 배치 정규화 (Batch Normalization) 란? 배치 정규화는 2015년 arXiv에 발표된 후
eehoeskrap.tistory.com
https://gaussian37.github.io/dl-concept-batchnorm/
배치 정규화(Batch Normalization)
gaussian37's blog
gaussian37.github.io
Batch Normalization 설명 및 구현
NIPS (Neural Information Processing Systems) 는 머신러닝 관련 학회에서 가장 권위있는 학회들 중 하나이다. 이 학회에서는 매년 컨퍼런스를 개최하고, 작년 12월에도 NIPS 2015라는 이름으로 러시아에서 컨
shuuki4.wordpress.com
https://lifeignite.tistory.com/47
Batch Normalization을 제대로 이해해보자
notion으로 보면 더 편합니다. www.notion.so/Batch-Normalization-0649da054353471397e97296d6564298 Batch Normalization Summary www.notion.so 목차 Summary Introduction Background Normalization Covariate Shift Batch Normalization Algorithm Learnable
lifeignite.tistory.com
'AI > Concepts' 카테고리의 다른 글
| Precision과 Recall이 반비례 관계인 이유에 대한 고찰 (1) | 2023.06.17 |
|---|---|
| Transfer Learning(pre-training, fine-tuning)의 개념에 대하여 (Prologue) (0) | 2023.02.04 |
| Activation이 Non-linearity를 갖는 이유 (0) | 2023.01.21 |
| Gradient Vanishing / Exploding에 대하여 (1) | 2023.01.17 |
| Back-Propagation(역전파)에 대하여 (1) | 2023.01.16 |



