| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 미래는_현재와_과거로
- NEXT
- 자바스크립트
- 백트래킹
- pytorch
- 크루스칼
- 분할 정복
- BFS
- c++
- 조합론
- 우선 순위 큐
- 너비 우선 탐색
- 다익스트라
- 플로이드 와샬
- dropout
- 세그먼트 트리
- lazy propagation
- 가끔은_말로
- tensorflow
- DP
- 알고리즘
- 문자열
- Overfitting
- 가끔은 말로
- 2023
- object detection
- 회고록
- dfs
- back propagation
- 이분 탐색
- Today
- Total
Doby's Lab
Back-Propagation(역전파)에 대하여 본문
✅ Contents
- 1. Intro
- 2. Gradient Descent
- 3. Back Propagation (1): MLP 구조 및 함수 정의
- 4. Back Propagation (2): \(w_{1,1}^{(2)}\) 업데이트
- 5. Back Propagation (3): \(w_{1,1}^{(1)}\) 업데이트
- 6. Outro
- 7. Reference
✅ 1. Intro
Batch Normalization에 대해 공부하다가 Gradient Vanishing / Exploding라는 개념이 다시 나왔었습니다.
Vanishing / Exploding 문제는 매우 낮거나, 높은 Learning Rate로 인해 발생하는 문제라고만 인식했었는데
Back-Propagation이 원인이 될 수 있다는 얘기가 나왔었습니다.
또한, Back-Propagation에 대해서는 Cost Function에 대한 값으로 인해 가중치가 Gradient Descent를 통해 변경되는 것만 알았지 정확히 어떤 원리에 이루어지는지는 몰랐기 때문에 정리를 해보려 합니다.
✅ 2. Gradient Descent
Gradient Descent는 앞서 포스팅을 통해 어떠한 원리를 통해 이루어지는지 알아본 바가 있습니다.
https://draw-code-boy.tistory.com/439
Gradient Descent와 Loss Function의 관계
Stochastic Gradient Descent를 공부할 때, Loss Function과의 관계가 궁금했습니다. 알고 나니 크게 어려운 건 없었지만 Gradient Descent에 대해 정리하며 관계까지 정리해보겠습니다. 해당 포스트는 아래 링크
draw-code-boy.tistory.com
또한, Gradient Descent를 통해 가중치가 어떻게 업데이트되는지도 잘 알고 있습니다.
$$ W := W - \alpha \frac{\partial }{\partial W}J_{total} $$
사실 이러한 사실만 알고 있다면 Back Propagation이 어떻게 이루어지는지 쉽게 알 수 있습니다.
이게 전부이니까요. 다만 이 과정 속에서 조금 디테일을 보고 싶었습니다.
✅ 3. Back Propagation (1): MLP 구조 및 함수 정의
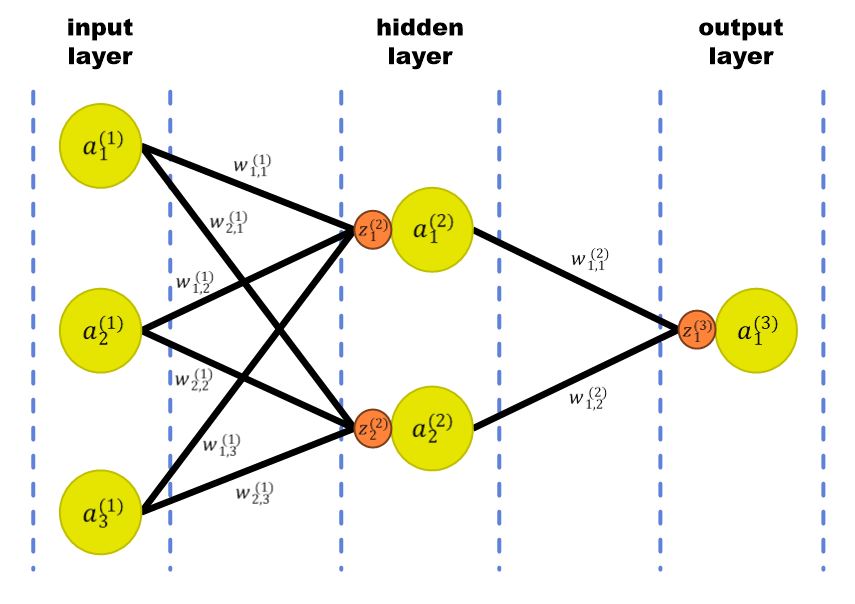
가중치가 어떻게 업데이트되는지 알기 때문에 간단한 MLP(Multi-Layer Perceptron) 구조를 가져와서 설명해 보겠습니다.

3-2-1 구조의 MLP입니다. 노란색 노드는 입력 값을 의미하며, 주황색 노드는 활성화 함수를 의미합니다.
이 구조에서는 sigmoid function을 사용한다고 가정하겠습니다. -> \(\phi(x)\)
또한, Cost function은 제곱값 오차를 쓴다고 가정하겠습니다. -> \(\frac{1}{2}(\hat{y} - y)^2\)
마지막으로 가중치, 출력 노드, 활성화 함수 등 여러 표기법은 Reference로 참고한 자료의 표기법을 이용해 설명하겠습니다.
(https://blog.naver.com/samsjang/221033626685)
표기법을 따르겠다는 것은 입력층의 각 노드에 대해 l층의 i번째 노드라면, \(a_{i}^{(l)}\) 로 정의하고,
가중치에 대해서는 i번째 노드에서 j번째 노드로 가는 l층에서 l+1층으로 향하는 가중치라면, \(w_{j,i}^{(l)}\)로 정의하겠습니다.
또한, Activation function은 l층으로 들어가는 i번째 함수라면, \(z_{i}^{(l)}\)로 정의하겠습니다.
$$ \begin{align}
a_{i}^{(l)} &= (input) \\ \\
w_{j,i}^{(l)} &= (weight) \\ \\
z_{i}^{(l)} &= (activation)
\end{align} $$
위와 같이 정리한 것들을 MLP의 구조 그림에 나타내면 아래와 같은 그림입니다.
✅ 4. Back Propagation (2): \(w_{1,1}^{(2)}\) 업데이트
이제 구조에 대해 알았고, 필요한 변수 및 함수들을 정의했으니 한 가중치에 대해 업데이트가 어떻게 이루어지는지 알아봅시다.
📄 4.1. 특정 가중치가 영향을 끼치는 모든 Cost function에 대해 생각할 것
업데이트할 때 중요하게 알아야 할 건 특정 가중치가 영향을 끼치는 손실에 대해 모두 따져보아야 합니다.
즉, 주어진 예시에선 다가오지 않겠지만 output layer의 노드가 2개였다고 생각해 봅시다.
그러면 \(\{w_{1,1}^{(2)},\;w_{2,1}^{(2)},\;w_{1,2}^{(2)},\;w_{2,2}^{(2)}\}\)과 같은 가중치들이 생겨났을 겁니다.
또한, output layer의 노드가 2개임에 따라 Cost function도 \(J_{total} = J_1 + J_2\)와 같이 나뉘었겠죠.
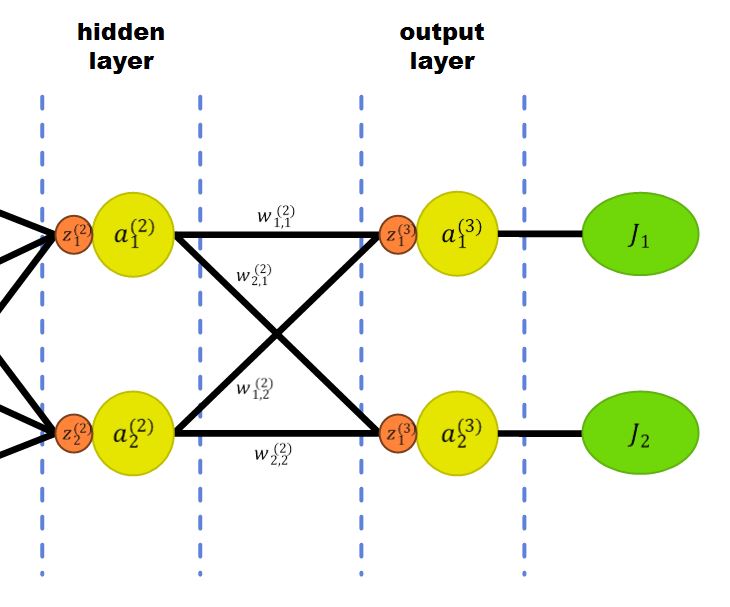
그러면 이러한 상황에서는 \(w_{1,1}^{(2)}\)이 \(J_1\)에만 영향을 끼치기 때문에 \(w_{1,1}^{(2)}\)을 업데이트할 때는 \(w_{1,1}^{(2)}\)에 대한 \(J_1\)의 변화율만 생각해 주면 됩니다.
$$ w_{1,1}^{(2)} = w_{1,1}^{(2)} - \alpha \frac{\partial J_1}{\partial w_{1,1}^{(2)}} $$
추가적으로 \(w_{1,1}^{(1)}\)같은 경우는 \(J_1\)와 \(J_2\) 둘 다 영향을 미치기 때문에 아래와 같이 변화율에 대해 신경 써줘야 합니다.
$$ w_{1,1}^{(1)} = w_{1,1}^{(1)} - \alpha (\frac{\partial J_1}{\partial w_{1,1}^{(2)}} + \frac{\partial J_2}{\partial w_{1,1}^{(1)}}) $$
📄 4.2. 본론
그럼 이제 다시 본론으로 돌아오겠습니다.
처음에는 \(w_{1,1}^{(2)}\)의 업데이트를 알아보겠습니다. 현재 MLP는 output layer의 노드가 하나이기 때문에
\(w_{1,1}^{(2)}\)의 업데이트는 아래와 같이 이루어집니다.
계산이 간단하게 이루어지기 위해 \(\alpha\)(=Learning Rate)는 1로 간주하겠습니다.
$$ w_{1,1}^{(2)} = w_{1,1}^{(2)} - \frac{\partial J_{total}}{\partial w_{1,1}^{(2)}} $$
\(\frac{\partial J_{total}}{\partial w_{1,1}^{(2)}}\)를 구하면 가중치에 따른 손실 함수의 변화율을 구할 수 있습니다.
대략적으로 \(w_{1,1}^{(2)}\)와 \(J_{total}\)은 아래와 같은 관계를 가집니다.
$$ J_{total}(a_1^{(3)}(z_1^{(3)}(w_{1,1}^{(2)}))) $$
이 식을 보면 확실히 관계에 대해 이해가 갈 겁니다.
또한, 그림으로는 아래와 같이 나타낼 수도 있습니다.
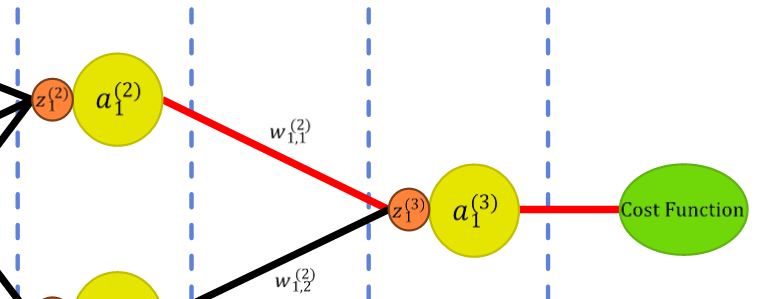
그래서 이 관계에 대한 변화율, 즉 미분을 구하면 얼마나 변할 지에 대한 값을 알 수 있습니다.
합성함수를 미분하기 위해서는 미분의 연쇄법칙(Chain Rule)에 대해 알고 있어야 합니다.
이에 관해서는 아래에 정리해 두었습니다.
https://draw-code-boy.tistory.com/517
미분의 연쇄 법칙(Chain Rule)에 대하여
Gradient Vanishing 현상에 대해 공부하던 중에 Back Propagation의 작동 원리에 대해 알아야 했고, 이 과정에서 미분의 연쇄 법칙이 쓰여 정리해 봅니다. 미분의 연쇄 법칙(Chain Rule) 미분의 연쇄 법칙이란
draw-code-boy.tistory.com
연쇄 법칙에 의해 미분을 하면 아래와 같은 결과가 나오게 됩니다.
$$ \frac{\partial J_{total}}{\partial w_{1,1}^{(2)}}
= \frac{\partial J_{total}}{\partial a_1^{(3)}}
\times\frac{\partial a_1^{(3)}}{\partial z_1^{(3)}}
\times\frac{\partial z_1^{(3)}}{\partial w_{(1,1)}^{(2)}} $$
이제 오른쪽 식의 각 항들에 대해 알아보겠습니다.
4.2.1. First Term
$$ \frac{\partial J_{total}}{\partial a_1^{(3)}}
= \frac{1}{2}\frac{\partial}{\partial a_1^{(3)}}
(a_1^{(3)}-y_1)^2
= (a_1^{(3)}-y_1) $$
손실함수의 입력 값에 대해 미분이므로 그대로 미분해 주면 됩니다.
4.2.2. Second Term
$$ \frac{\partial a_1^{(3)}}{\partial z_1^{(3)}}
= \phi(z_1^{(3)})(1-\phi(z_1^{(3)}))
= a_1^{(3)}(1-a_1^{(3)}) $$
시그모이드 함수의 입력 값에 대한 미분입니다.
시그모이드 함수 미분의 결과가 왜 저렇게 나오는지 궁금하다면 아래의 몫의 미분법에 대한 포스팅을 참고하시길 바랍니다.
또한, \(\phi(z_1^{(3)})\)가 \(a_1^{(3)}\)이 나오는 이유는 애초에 \(z_1^{(3)}\)의 시그모이드 함수에 대한 결과가 \(a_1^{(3)}\)이기 때문입니다.
https://draw-code-boy.tistory.com/518
몫의 미분법(Quotient Rule)에 대하여
Back Propagation에 대해 공부하다가 시그모이드 함수의 미분에 대해 '어떻게 미분을 했길래 이런 결과가 나오는 거지'라는 궁금증이 생겨 정리하게 되었습니다. 몫의 미분법(Quotient Rule) 몫의 미분법
draw-code-boy.tistory.com
4.2.3. Third Term
$$ \frac{\partial z_1^{(3)}}{\partial w_{1,1}^{(2)}}
= a_1^{(2)} $$
다음과 같은 결과가 나오는 이유는 \(z_1^{(3)} = w_{1,1}^{(2)}a_1^{(2)} + X\)로 이루어져 있습니다.
당연하게도 \(w_{(1,1)}^{(2)}\)의 변화에 따른 \(z_1^{(3)}\)의 변화율은 \(a_1^{(2)}\)가 결정짓습니다.
4.2.4. Result Term
$$ \frac{\partial J_{total}}{\partial w_{1,1}^{(2)}} = (a_1^{(3)}-y_1)\times a_1^{(3)}(1-a_1^{(3)})\times a_1^{(2)} $$
총변화율은 위와 같이 정리될 수 있습니다.
즉, 역전파에서 가중치의 업데이트를 위해 사용되는 오차의 가중치에 대한 미분값이 결국 역전파에서 출발노드의 활성화 함숫값과 도착 노드의 활성화 함숫값, 그리고 실제 값만으로 표현되는 것을 알 수 있습니다.
✅ 5. Back Propagation (3): \(w_{1,1}^{(1)}\) 업데이트
이번엔 \(w_{1,1}^{(1)}\)의 업데이트에 대해 알아보겠습니다.
📄 5.1. 중복적인 부분
\(w_{1,1}^{(1)}\)의 업데이트를 하려면 \(w_{1,1}^{(1)}\)가 변함으로써 영향을 받는 모든 변수들을 알아야 합니다.
영향을 받는 변수들을 아래 그림과 같겠네요.

그런데 \(w_{1,1}^{(2)}\)와 중복적인 부분들이 많이 보입니다.
함성함수로 나타내면 아래와 같습니다.
$$ J_{total}(a_1^{(3)}(z_1^{(3)}({a_1^{(2)}(z_1^{(2)}(w_{1,1}^{(1)})})))) $$
이 함수를 미분하면 아래와 같이 나옵니다.
$$ \frac{\partial J_{total}}{\partial w_{1,1}^{(1)}}
= \frac{\partial J_{total}}{\partial a_1^{(3)}}
\times\frac{\partial a_1^{(3)}}{\partial z_1^{(3)}}
\times\frac{\partial z_1^{(3)}}{\partial a_1^{(2)}}
\times\frac{\partial a_1^{(2)}}{\partial z_1^{(2)}}
\times\frac{\partial z_1^{(2)}}{\partial w_{1,1}^{(1)}} $$
5.1.1. First Term & Second Term (중복 부분)
그런데 여기서 \(\frac{\partial J_{total}}{\partial a_1^{(3)}}
\times\frac{\partial a_1^{(3)}}{\partial z_1^{(3)}}\)는 앞서 구한 바가 있습니다.
그럼 이걸 다시 계산해야 할까요?
아닙니다. 간단한 모델로 표현했을 뿐, 실제로는 깊은 layer들로 이루어진 모델들이 주를 이룹니다.
그래서 이런 중복 부분을 역전파로 넘기면서 계산을 줄입니다. 이것도 역전파 알고리즘의 핵심 기능 중 하나입니다.
그럼 식에서 오른쪽 2개의 항은 중복된 부분으로 넘어왔고, 나머지 3개만 계산해 주면 될 거 같습니다.
5.1.2. Third Term
$$ \frac{\partial z_1^{(3)}}{\partial a_1^{(2)}}=w_{1,1}^{(2)} $$
\(w_{1,1}^{(1)}\)의 Third Term을 업데이트를 할 때와 같은 이유로 미분 값은 \(w_{1,1}^{(2)}\)입니다.
5.1.3. Fourth Term
$$ \frac{\partial a_1^{(2)}}{\partial z_1^{(2)}}
= \phi(z_1^{(2)})(1-\phi(z_1^{(2)}))
= a_1^{(2)}(1-a_1^{(2)}) $$
시그모이드 함수에 대한 미분으로 다음과 같이 정리되었습니다.
5.1.4. Fifth Term
$$ \frac{\partial z_1^{(2)}}{\partial w_{1,1}^{(1)}}
= a_1^{(1)} $$
\(w_{1,1}^{(1)}\)의 Third Term을 업데이트를 할 때와 같은 이유로 미분 값은 \(a_1^{(1)}\)입니다.
5.1.5. Result Term
$$ (a_1^{(3)}-y_1)\times a_1^{(3)}(1-a_1^{(3)})
\times w_{1,1}^{(2)} \times a_1^{(2)}(1-a_1^{(2)})
\times a_1^{(1)} $$
총변화율은 위와 같이 정리됩니다. 보기에 복잡한 식이기 때문에 중복된 부분\(\frac{\partial J_{total}}{\partial a_1^{(3)}}
\times\frac{\partial a_1^{(3)}}{\partial z_1^{(3)}}\)을 l층의 i번 노드에서 보낸다 하여 \(\delta_{i}^{(l)}\)라 요약한다면,
총변화율을 아래와 같이 정리될 수 있습니다.
$$\begin{align}
\frac{\partial J_{total}}{\partial w_{1,1}^{(1)}}
&= \delta_{1}^{(3)}
\times\frac{\partial z_1^{(3)}}{\partial a_1^{(2)}}
\times\frac{\partial a_1^{(2)}}{\partial z_1^{(2)}}
\times\frac{\partial z_1^{(2)}}{\partial w_{1,1}^{(1)}} \\ \\
&= \delta_{1}^{(3)}
\times w_{1,1}^{(2)} \times a_1^{(2)}(1-a_1^{(2)})
\times a_1^{(1)}
\end{align} $$
📄 5.2. input layer의 \(w_{1,2}^{(1)},\;w_{1,3}^{(1)}\)
\(w_{1,2}^{(1)},\;w_{1,3}^{(1)}\) 이 두 개의 가중치가 학습하는 방법은 \(w_{1,1}^{(1)}\)를 구하면서 이미 많이 중복된 항들이 많기 때문에 알맞은 미분값만 바꾸어 기존의 중복 부분에다가 곱해주면 됩니다.
$$ \begin{align}
\frac{\partial J_{total}}{\partial w_{1,2}^{(1)}}
&= \delta_{1}^{(3)}
\times\frac{\partial z_1^{(3)}}{\partial a_1^{(2)}}
\times\frac{\partial a_1^{(2)}}{\partial z_1^{(2)}}
\times\frac{\partial z_1^{(2)}}{\partial w_{1,2}^{(1)}} \\ \\
&= \delta_{1}^{(3)}
\times w_{1,1}^{(2)} \times a_1^{(2)}(1-a_1^{(2)})
\times a_2^{(1)}
\end{align} $$
$$ \begin{align}
\frac{\partial J_{total}}{\partial w_{1,3}^{(1)}}
&= \delta_{1}^{(3)}
\times\frac{\partial z_1^{(3)}}{\partial a_1^{(2)}}
\times\frac{\partial a_1^{(2)}}{\partial z_1^{(2)}}
\times\frac{\partial z_1^{(2)}}{\partial w_{1,3}^{(1)}} \\ \\
&= \delta_{1}^{(3)}
\times w_{1,1}^{(2)} \times a_1^{(2)}(1-a_1^{(2)})
\times a_3^{(1)}
\end{align} $$
📄 5.3. 알아두어야 할 점
input layer에 가까워질수록 가중치를 변경하는 항에 대해 곱해지는 미분 값들이 엄청 많아지는 것을 꼭 알고 있어야 합니다.
그리고, 곱해지는 미분 값들 중에서는 sigmoid 함수의 미분이 계속 곱해지고 있었다는 것을 중요하게 생각합시다.
다음 포스팅에서는 sigmoid 함수를 Activation function으로 둠으로써 발생할 수 있는 Gradient Vanishing/Exploding에 대해 다루어보겠습니다.
✅ 6. Outro
복잡한 개념에 대해 설명하다보니 글이 엄청 길어지고, PPT도 많이 사용하며 MathJax도 엄청 사용한 거 같습니다.
그래도 블로그를 통해 한 번 더 정리를 하다보니 제 것으로 더 깊게 만들 수 있는 계기가 되었던 거 같습니다.
레퍼런스로 가져온 글들이 너무 좋아서 레퍼런스 글들도 읽어보셨으면 좋겠습니다.
글이 길어지게 되어 Outro라도 적어야 할 거 같아 글을 남깁니다:)
✅ 7. Reference
https://blog.naver.com/samsjang/221033626685
[35편] 딥러닝의 핵심 개념 - 역전파(backpropagation) 이해하기1
1958년 퍼셉트론이 발표된 후 같은 해 7월 8일자 뉴욕타임즈는 앞으로 조만간 걷고, 말하고 자아를 인식하...
blog.naver.com
딥러닝의 핵심, 역전파
역전파(Back Propagation)란 무엇일까? 역전파의 의미 우선 역전파의 정의에 대해서 알아보자. 역전파는 신경망의 각 노드가 가지고 있는 가중치(Weight)와 편향(Bias)을 학습시키기 위한 알고리즘으로,
re-code-cord.tistory.com
[DL] 역전파 알고리즘(backpropagation algorithm)
이번 글은 오차 역전파 알고리즘(backpropagation algorithm)에 대해 공부하고 정리해보도록 하겠습니다.신경망에서 경사 하강법을 적용할 때 손실 함수에서 각 가중치까지 신경망의 역방향으로 실행
velog.io
'AI > Concepts' 카테고리의 다른 글
| Activation이 Non-linearity를 갖는 이유 (0) | 2023.01.21 |
|---|---|
| Gradient Vanishing / Exploding에 대하여 (1) | 2023.01.17 |
| Batch Normalization이란? (Basic) (0) | 2023.01.02 |
| Dropout에 대하여 (1) | 2022.12.31 |
| L1, L2 Regularization에 대하여 (0) | 2022.12.31 |




