| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 분할 정복
- Overfitting
- 회고록
- pytorch
- back propagation
- dropout
- NEXT
- 가끔은 말로
- 플로이드 와샬
- BFS
- 다익스트라
- c++
- 자바스크립트
- 조합론
- tensorflow
- object detection
- 문자열
- 이분 탐색
- 2023
- 백트래킹
- 우선 순위 큐
- lazy propagation
- 알고리즘
- 크루스칼
- DP
- 세그먼트 트리
- dfs
- 너비 우선 탐색
- 미래는_현재와_과거로
- 가끔은_말로
- Today
- Total
Doby's Lab
Gradient Descent와 Loss Function의 관계 본문
Stochastic Gradient Descent를 공부할 때, Loss Function과의 관계가 궁금했습니다. 알고 나니 크게 어려운 건 없었지만 Gradient Descent에 대해 정리하며 관계까지 정리해보겠습니다.
해당 포스트는 아래 링크 영상에 관한 정리 내용입니다.
(https://www.youtube.com/watch?v=h6aath0ulX4 )
Loss Function
Loss Function이란 Model이 내놓는 예측 값과 실제 값의 차이를 얻어내는 메커니즘입니다. 예측 값과 실제 값의 차이를 Error라고 합니다. 엔지니어의 입장에서는 이러한 Error를 최소화시키는 방향으로 Model을 구현해야 합니다.
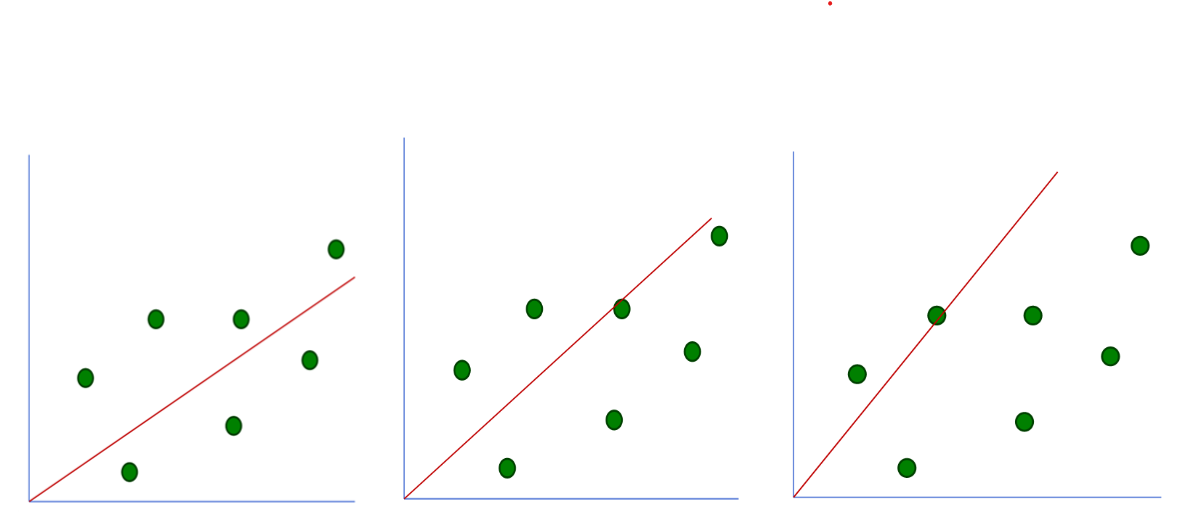
간단히 설명하기 위해 Linear Regression Model을 하나 가져와보겠습니다.

데이터를 학습함에 따라 빨간 선과 같은 Model Parameter(=선형 방정식)이 만들어집니다. 이 Parameter가 내놓는 예측 값과 실제 값의 차이가 최소가 되게 만들어야 합니다. 다시 말하자면 선형 방정식에 대입하는 X값에 대한 Y값이 실제 데이터의 Target과의 차이가 최소가 되어야 한다는 뜻입니다. 지금 설명은 아래와 같습니다.

Loss Function은 종류에 따라 모델이 달라집니다. Logistic loss function(= binary cross-entrophy function)은 Binary Classification을, Cross-entrophy loss function은 Multiple Classification으로 모델이 나뉩니다.
Gradient Descent
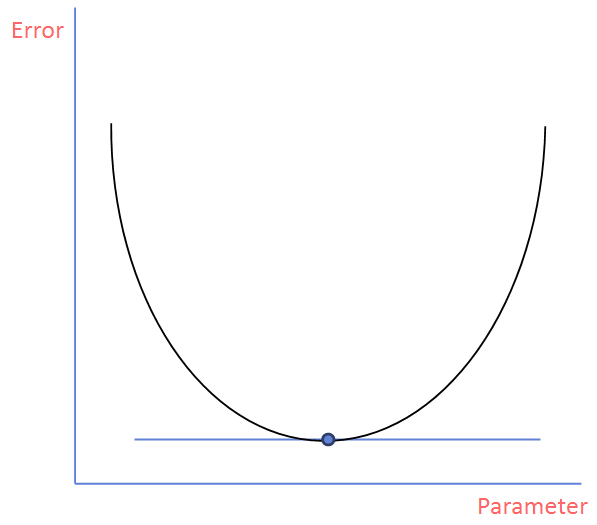
Loss Function이 최소화가 되게 하려면 자연스럽게 드는 생각은 '아래 그림처럼 모든 기울기에 대해 Brute-Force 하게 탐색해봐야 할까?'라는 생각입니다. 이러면 계산량도 많아지고, 또한 시간도 오래 걸리는 작업이 됩니다.
이런 문제를 Gradient Descent로 해결할 수 있습니다. Gradient Descent는 한국말로 '경사 하강법'이라고 합니다. 왜 경사를 하강하는지 알아보고, 그 방법이 왜 시간을 줄여주는지 알아봅시다.
선형 방정식의 기울기에 따라서 Error값을 나타내면 아래와 같이 나타날 수 있습니다.
(X축은 기울기지만 또 한 번 기울기에 대해 다루기 때문에 X축은 Parameter라고 하겠습니다.)

우리는 Error값이 최소가 되어야 하기 때문에 아래 그림과 같이 Parameter를 구하면 좋을 거 같습니다.
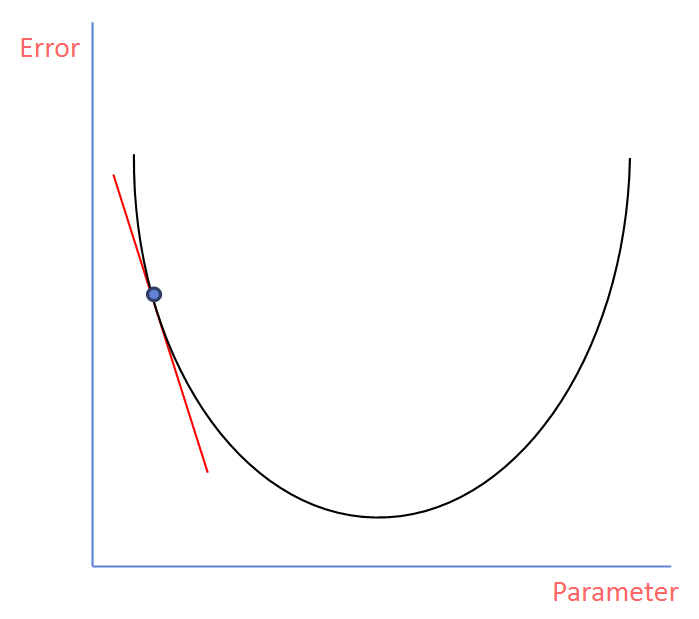
하지만, 단번에 이 값을 찾을 수 없기에 최적 값을 찾아가는 과정에 대해 알아봅시다. 우선 랜덤 하게 Parameter가 주어지면 아래와 같이 해당 점에서 미분 값을 구합니다. 그리고, 이 미분 값은 이 표의 그래프에 대해 기울기가 됩니다.
이 기울기를 가지고서 다음 Parameter를 찾아갈 수 있습니다. 다음 Parameter를 찾아가기 위해서는 아래 과정을 거칩니다.
- 기울기가 얼마나 가파른지(=절댓값이 얼마나 큰지)에 따라서 다음 Parameter로 갈 거리를 지정
- 기울기가 음수 or 양수에 따라 방향을 지정
다음 과정을 여러 번 반복하여 거친다면 모든 기울기에 대해 탐색할 필요 없이 점점 아래로 내려가 원하는 최적의 Parameter값을 찾을 수 있겠습니다.
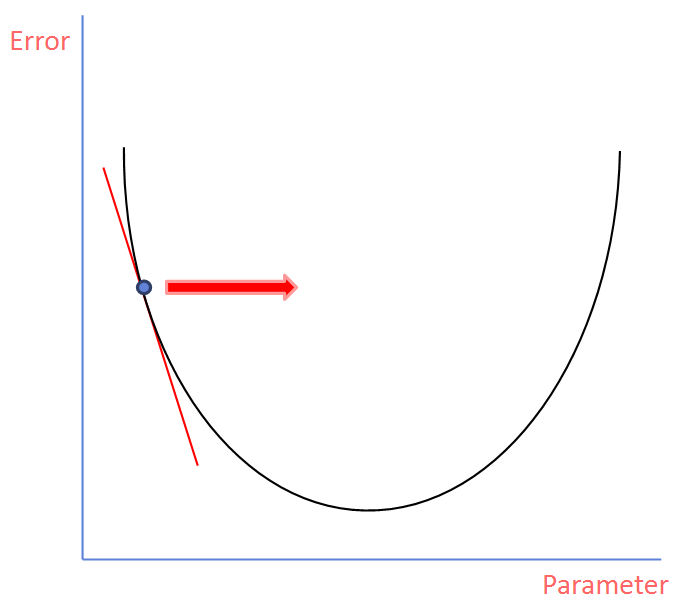
이런 과정을 가파른 경사에서 하강하는 것과 같다 하여 Gradient Descent라고 부릅니다. 즉, 적절한 Parameter를 빠르게 찾기 위한 방법이라고 할 수 있겠습니다.
Note
정리하자면 Loss Function은 실제 값과 예측 값의 차이를 얻어내는 메커니즘이라 할 수 있고, Loss Function을 최소화하기 위해 Model Parameter를 만들 때, 빠르게 만들기 위해 Gradient Descent를 사용합니다.
'AI > Concepts' 카테고리의 다른 글
| Dropout에 대하여 (1) | 2022.12.31 |
|---|---|
| L1, L2 Regularization에 대하여 (0) | 2022.12.31 |
| Image Augmentation이란? (2) | 2022.12.29 |
| Normalization이 필요한 이유 (1) | 2022.12.28 |
| Standardization(표준화)와 Normalization(정규화)의 차이 (0) | 2022.09.03 |




