| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 세그먼트 트리
- 백트래킹
- back propagation
- object detection
- 플로이드 와샬
- 회고록
- 알고리즘
- 우선 순위 큐
- NEXT
- 크루스칼
- c++
- lazy propagation
- 분할 정복
- BFS
- 너비 우선 탐색
- 2023
- 자바스크립트
- 문자열
- 다익스트라
- dfs
- 조합론
- 이분 탐색
- Overfitting
- DP
- tensorflow
- 가끔은 말로
- dropout
- 미래는_현재와_과거로
- 가끔은_말로
- pytorch
- Today
- Total
Doby's Lab
Precision과 Recall이 반비례 관계인 이유에 대한 고찰 본문
✅ Intro
블로그를 보면서 복습 중에 Precison과 Recall이 반비례 관계인 이유가 궁금해졌습니다. 수식적으로 보았을 때, 이해가 되지 않는 부분이 있어서 다른 관점들을 통해 조금이나마 접근을 다르게 해 보았습니다.
https://draw-code-boy.tistory.com/531
mAP (mean Average-Precision)에 대하여
일반적으로 Object Detector의 성능이 얼마나 좋은지에 대한 지표로는 mAP가 널리 쓰이고 있습니다. 오늘은 mAP는 어떻게 도출되는 결과인지에 대해 알아보겠습니다. ✅ Precision(정확도), Recall(검출율,
draw-code-boy.tistory.com
✅ Question
Precision(정확도)와 Recall(검출율)에 대한 수식은 아래와 같다는 것을 알고 있었습니다.
$$ Precision = \frac{TP}{TP+FP} = \frac{TP}{All\;Detections} $$
$$ Recall = \frac{TP}{TP+FN} = \frac{TP}{All\;Ground\;Truth} $$
두 지표가 반비례라는 것은 Precision이 상승할 때, Recall은 올라간다는 것을 의미합니다. 반대의 경우도 마찬가지입니다.
하지만, 수식으로 보았을 때 Precision이 올라간다는 것은 FP가 낮아진다는 것이고, 즉 TN이 올라가는 것으로 해석할 수 있었습니다. 그런데 TN이 올라가는 것이 Recall이 낮아지는 것과 무슨 연관성을 가지냐는 것이 포스트의 요인입니다.
✅ Answer
여러 포스팅을 보았지만, 수식에 대한 명쾌한 답은 없었습니다. 그러나, Precision과 Recall이라는 개념에 대해 접근하는 관점이 다른 부분들에 대해서 '아 이렇게 보면 반비례 관계가 맞는구나'라는 것들이 꽤 있었습니다.
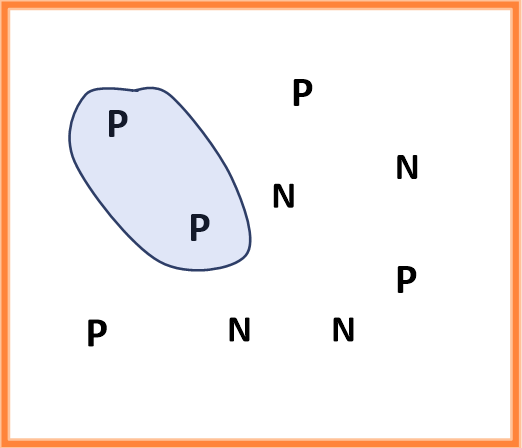
한 케이스를 예를 들어 설명하겠습니다. 아래와 같이 P(Positive)가 5개와 N(Negative)이 4개인 데이터들이 있습니다.

Detector가 아래와 같이 감지했다면, Recall은 100%지만, Precision은 55.55%(5/9) 밖에 되질 않습니다.
Detector가 가지고 있는 조건이 까다롭지 않은지 검출은 많이 해내지만 정확도는 떨어집니다.

이번엔 Precision이 100%로 올라갔지만, Recall은 40%(2/5)밖에 되질 않습니다.
이번 Detector는 조건이 꽤나 까다로운지 Positive를 많이 검출해 내지 못합니다.
이처럼 둘 중 하나가 높으면 다른 하나가 낮아지는 반비례 관계를 확인할 수 있습니다.
그래서 아까 수식에서 이해 안 되었던 부분이 'FP가 낮아지고, TN이 올라가는 것이 무슨 연관이냐'라는 질문에 대한 답은
FP가 낮아진다는 것은 전반적으로 Positive로 검출하는 조건이 까다로워져서라는 것입니다. 즉, FP가 왜 낮아진 것에 대한 원인을 도출해 낸다면 반비례 관계임을 알 수 있습니다.
또한, Positive로 검출하는 것이 적다는 말은 Detector가 매우 까다로운 조건을 가지고 있다는 것입니다. 그래서 Precision은 높지만, Recall은 낮은 것입니다.
결론적으로, Precision과 Recall 모두 모델을 평가하는 데에 있어서 필요합니다.
정확도는 높은데 많이 검출을 못 해내는 경우, 검출은 많이 해내는데 정확도가 떨어지는 경우 이 두 가지 모두 중요시하게 봐야 되기 때문에 많은 모델을 비교하기 위해 둘을 합친 PR Curve를 이용한 mAP를 사용합니다.
✅ Answer 2 (23.07.14 Update)
앞선 포스팅에서 Precision과 Recall이 반비례하는 이유에 대해 각 지표의 수식이 아닌 성질로 접근을 하여 이해를 할 수 있었습니다.
추가적인 업데이트의 이유는 기존 Precision의 도식화 오류와 성질로부터 수식의 이해가 가능했기에 작성을 하게 되었습니다.
- Question의 결론 (FP -> TN -> Recall의 관계)
- Precision의 도식화 오류
- 성질로부터 수식의 이해
📄 Question의 결론 (FP -> TN -> Recall의 관계)
들어가기 앞서 Question에서 반비례의 원인을 찾는 시작점은 'FP가 내려가는 것이 Recall이 올라가는 것과 무슨 연관이 있는가'이었습니다. 이 의문에 대해 결론을 짓고 넘어가겠습니다.
저의 생각으로 접근한 결과 'FP는 본질적으로 Negative 데이터라는 것을 나타내기 때문에 FP가 내려가는 것은 상반된 의미의 TN의 상승을 의미한다.'로 생각했습니다.
문제는 다시 'TN의 상승이 Recall의 상승에 영향을 미치는가'로 재정의 되었습니다.
Recall의 성질이자 의미는 '최대한 많은 양의 데이터를 Positive로 검출해내는가를 묻는 지표'이기 때문에 TN은 Recall의 상승에 영향을 미치지 않는다라고 생각하게 되었습니다.
📄 Precision의 도식화 오류
기존에 Precision이 높다라는 케이스를 위 그림과 같이 가정할 때, 아래와 같이 도식화함으로써 Precision을 그렸습니다.

하지만, 이 케이스의 경우에는 Precision이 높을 뿐만 아니라 Recall도 높은 케이스라는 것을 수식을 통해서도 알 수 있습니다. FP와 FN이 0으로 수렴하여 Precision = 100, Recall = 100이 되기 때문입니다.
그래서 Precision이 독단적으로 높은 케이스를 고려할 때는 'Detector가 예민하다'라는 성질을 인지하여 아래와 같이 고려해야 합니다.

📄 성질로부터 수식의 이해
간단하게 두 지표에 대해 성질을 정리하면, Precision은 예민한 Detector를 나타내는 지표, Recall은 관대한 Detector를 나타내는 지표로 해석이 됩니다.
이러한 성질로 두 지표의 반비례 관계를 이해할 수 있게 되었고, 이제는 수식의 반비례 관계까지 이해할 수 있게 되었습니다.
Precision이 독단적으로 높은 케이스를 생각해 봅시다. 아래와 같이 FN의 비율(빨간 원)이 높아진다는 것을 캐치한다면 Precision이 높을 때, Recall이 낮아지는 원인에 대해 도출할 수 있습니다.

최종적으로, 기존의 수식으로 반비례의 원인을 찾지 못했던 이유는 📄 Precision의 도식화 오류가 있었기 때문입니다.
'AI > Concepts' 카테고리의 다른 글
| Entropy와 Gini Impurity에 대하여: Decision Tree는 어떻게 만들어질까, Classification (1) | 2023.07.27 |
|---|---|
| Label Encoding의 문제점 (with Chat GPT) (0) | 2023.07.20 |
| Transfer Learning(pre-training, fine-tuning)의 개념에 대하여 (Prologue) (0) | 2023.02.04 |
| Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift (4) | 2023.01.22 |
| Activation이 Non-linearity를 갖는 이유 (0) | 2023.01.21 |


