| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 백트래킹
- pytorch
- 가끔은_말로
- c++
- object detection
- 2023
- 분할 정복
- lazy propagation
- DP
- 이분 탐색
- 우선 순위 큐
- 세그먼트 트리
- tensorflow
- back propagation
- dropout
- 크루스칼
- Overfitting
- 가끔은 말로
- 문자열
- NEXT
- BFS
- 조합론
- 알고리즘
- 플로이드 와샬
- dfs
- 자바스크립트
- 다익스트라
- 너비 우선 탐색
- 회고록
- 미래는_현재와_과거로
- Today
- Total
Doby's Lab
RMS Normalization, ICS의 해결책은 re-scaling에 있다. 본문
✅ Intro
기존 Layer Normalization을 통해서 internal covariate shift 현상(레이어를 통과함에 따라 데이터의 분포가 달라지는 현상)을 해결하며, 이를 통해 심층 신경망 구조의 네트워크는 학습을 더 안정화시키고, 최적의 loss까지 빠르게 수렴하도록 도와줍니다. 하지만, Layer Normalization은 computational overhead(연산 자원)을 많이 필요로 하며, 결과적으로 이것은 학습의 속도를 낮추게 됩니다.
이러한 문제점에 기반하여 'Root Mean Square Layer Normalization'이라는 논문에서는 RMS Normalization을 제안합니다. 개념에 대해서는 아래에서 다루지만, 이 연구의 결과는 학습의 속도적인 문제점을 해결하는 데에 있어 LLM의 학습에 많이 쓰입니다.
✅ Layer Normalization
Layer Normalization을 이해하기 위해서 m차원의 벡터를 가지는 input \(X\)와 Linear transform과 Activation function,\(f(\cdot)\)을 통과한 n차원을 가지는 output을 \(Y\)라 가정합시다. 그러면, \(X\), \(Y\), 그리고 Linear transform을 위한 가중치 \(W\) 행렬은 아래와 같습니다.
$$ \begin{align}
x=&\left[x_1, x_2,\dotso,x_m\right] \\
\\
w =& \begin{bmatrix}
w_{1,1} & \dotsm & w_{1,n} \\
\vdots & \ddots & \vdots \\
w_{m,1} & \dotsm & w_{m,n} \\
\end{bmatrix} \\
\\
x\times w=&\:a=[a_1, a_2,\dotso,a_n] \\
\\
y_i =& f(a_i+b_i)
\end{align} $$
위 과정에서 결과 \(Y\)를 구할 때, Internal Covariate Shift가 발생합니다.

그래서, Layer Normalization에서는 레이어를 통과함에 따라 데이터의 분포가 달라지는 현상을 해결하기 위해서 가중치를 통과한 벡터 \(a\)의 평균 \(\mu\)와 분산 \(\sigma\)를 구하고, gain parameter(init value = 1), \(g_i\)를 곱하여 데이터를 Standardization하여 데이터의 편향적인 분포를 처리하도록 합니다.
$$ \overline{a}_i=\frac{a_i-\mu}{\sigma}g_i,\:\: y_i=(\overline{a}_i+b_i) $$
✅ RMS Normalization
Layer Normalization이 Internal Covariate Shift를 해결하여, 모델의 성능을 높일 수 있는 이유를 본 논문에서는 데이터 분포의 re-centering과 데이터 자체의 re-scaling이라 언급하였습니다. 본 논문에서는 두 이점 중에서 re-scaling이 성공 요인일 것이라는 가설을 세워 RMS Normalization을 제안합니다.
이것이 의미하는 바는 레이어를 통과한 데이터에 대해서 편향적인 분포를 다시 정규 분포에 가깝게 자리 잡도록 하는 것을 re-centering이라 하고, 이 과정에서 데이터 값에 대해 스케일링이 이루어졌기에 re-scaling이라 합니다.
RMS Normalization은 레이어를 통과한 벡터 \(a\)에 대해서 RMS 값을 구하여 나누어주고, gain parameter \(g_i\)를 곱합니다.
$$ \overline{a_i} = \frac{a_i}{\text{RMS}(a)}g_i,\:\: \text{RMS}(a)=\sqrt{\frac{1}{n}\sum_{i=1}^{n}a_i^2} $$
re-centering을 할 필요 없이, re-scaling에 대해서만 집중하기 때문에 RMS를 통해 구할 수 있습니다.
또한, 평균과 분산을 계산할 필요가 없기 때문에 위 부분에서 언급한 Computational Overhead 문제를 해결할 수 있습니다.
추가적으로, 만약 Layer Normalization에서 평균이 0인 경우에는 수식을 고려해 보면, 결국에 RMS Normalization을 구하는 모양이 됩니다. 아래 평균과 분산을 구하는 수식을 보면 이해가 되실 겁니다.
$$ \mu=\frac{1}{n}\sum_{i=1}^{n}a_i,\:\:\sigma=\sqrt{\frac{1}{n}\sum_{i=1}^{n}(a_i-\mu)^2} $$
✅ 그래서 성능은 보장되는가?
Computational Overhead를 줄이는 것으로 RMS Nomalization을 제안했지만, 이것이 기존 Layer Nomralization과 성능이 유사하다는 것을 Valid BELU score를 측정하는 것을 통해서 밝혀냈습니다.
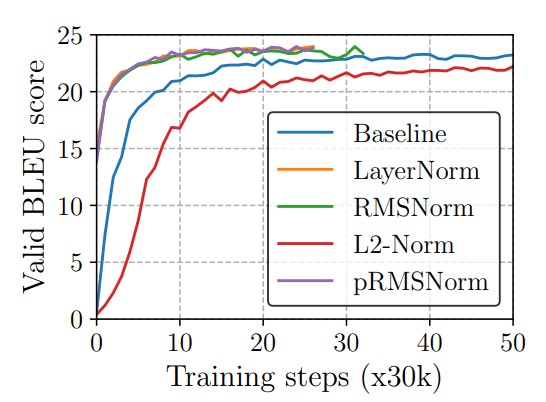
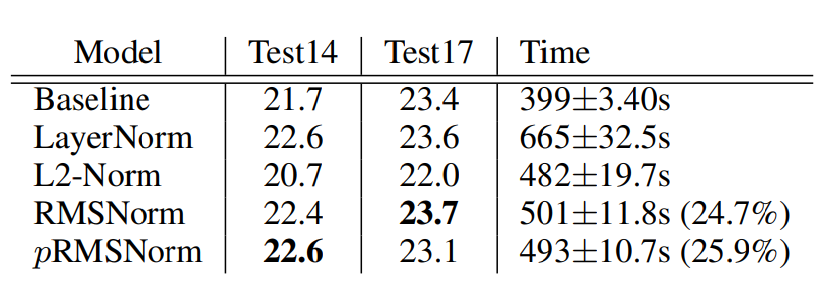
✅ Outro
기존 Layer Normalization에서 ICS를 해결하는 과정에서는 평균과 분산을 계속 구해야 하는 것 때문에 Computational head가 문제점이었습니다. RMS Normalization에서는 평균과 분산을 구하지 않고, RMS만을 계산하여 이 문제점을 해결하였고, 성능 또한 Layer Normalization에 준하게 나오는 것을 알 수 있었습니다.
✅ Reference
[1] Paper: 'Root Mean Square Layer Normalization'
'AI > Concepts' 카테고리의 다른 글
| Attention에 대해 Attention! (5) | 2023.12.26 |
|---|---|
| Entropy와 Gini Impurity에 대하여: Decision Tree는 어떻게 만들어질까, Classification (0) | 2023.07.27 |
| Label Encoding의 문제점 (with Chat GPT) (0) | 2023.07.20 |
| Precision과 Recall이 반비례 관계인 이유에 대한 고찰 (1) | 2023.06.17 |
| Transfer Learning(pre-training, fine-tuning)의 개념에 대하여 (Prologue) (0) | 2023.02.04 |



