| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- lazy propagation
- 회고록
- tensorflow
- 알고리즘
- DP
- 우선 순위 큐
- 세그먼트 트리
- BFS
- Overfitting
- 가끔은_말로
- 미래는_현재와_과거로
- 백트래킹
- object detection
- 2023
- 이분 탐색
- dfs
- pytorch
- 너비 우선 탐색
- 플로이드 와샬
- NEXT
- 문자열
- 크루스칼
- 가끔은 말로
- back propagation
- dropout
- c++
- 다익스트라
- 분할 정복
- 자바스크립트
- 조합론
- Today
- Total
Doby's Lab
Attention에 대해 Attention! 본문
✅ Introduction
ViT라는 아키텍처를 공부하다가 새로운 메커니즘을 접하게 되었습니다. 그 새로운 메커니즘은 이번 글의 주제인 Attention입니다. 아직 NLP 분야의 Task를 다루어본 경험이 없기 때문에 등장하게 된 정확한 배경은 잘 모르지만, '어떠한 작동 원리인가?', '왜 성능이 더 좋은가?', '수식이 의미는 무엇인가?'에 대해서 집중적으로 다루어 보고자 합니다.
기존 자연어처리 분야에서는 Recurrence mechanism, 비전 분야에서는 Convolutional mechanism으로 엄청난 연구 및 아키텍처들이 나온 만큼 이미 각 분야에서 각 mechanism이 탄탄한 베이스가 되어있었습니다. 하지만, '세상에 완벽한 시스템은 없다'라는 말과 같이 훌륭한 연구와 고질적인 문제들은 항상 공존해오고 있습니다.
그래서 고질적인 문제들 중 하나를 해결한 새로운 mechanism인 Attention에 대해서 정리를 해보고자 합니다.
✅ Problem
위에서 말한 기존 두 개의 mechanism의 문제점에 대해서 알아봅시다.
📄 Recurrence mechanism의 문제점
Recurrence mechanism의 문제점을 알아보려면, seq2seq의 구조를 살펴볼 필요가 있습니다. (seq2seq에 대한 전체적인 이해는 필요 없습니다.)
seq2seq은 구조적으로 보면, 크게 Encoder, Context vector, Decoder로 이루어지는데 Encoder를 통해 문장의 정보들이 압축되어 잘 담긴 Context vector를 만들어내고, 이를 Decoder에 넘겨서 문장을 번역하는 역할을 하는 모델입니다.

여기서 집중할 부분은 Encoder 부분입니다. 문장의 정보를 잘 담아내기 위해 LSTM 셀들이 다음 LSTM 셀에 정보를 넘겨줌과 동시에 다음 LSTM 셀의 순서에 해당하는 token(단어)를 입력으로 넣으면서 Context vector를 만들고 있습니다.
그런데 위 그림에서는 이해를 돕기 위해 "I am a student"라는 다소 간결한 문장으로 입력 시퀀스를 예시로 들었지만, 엄청나게 긴 문장이라면 엄청나게 많은 token들이 Context vector에 압축되어 담길 텐데 정보가 잘 보존이 될까요?
"Position embeddings are added to the patch embeddings to retain positional information." (ViT 논문에서 예시로 가져온 문장입니다.)
여기서 만약에 이 문장을 seq2seq의 Encoder로 넣었다 했을 때, 맨 앞 token인 "Position"은 이 문장에 있어서 중요한 역할을 합니다. "Position"이라는 token이 없다면, 무슨 embedding이 patch embedding에 더해져서 위치 정보를 보존하는지를 모르게 되니까요.
하지만, 저렇게 긴 문장에서 첫 시작을 알리는 token이 수많은 LSTM 셀에 의해 거쳐가면서 잘 보존이 될까요? Context vector에는 첫 token("Position")이 잘 반영이 되었을까요? 그렇다고 보기에는 어렵습니다.
이러한 긴 문장에 대해서 모든 token들이 LSTM 셀을 거치며 갈수록 잘 반영이 되지 않는 '장기 의존성 문제'와 많은 정보를 함축적으로 요약해야 했던 Context Vector에는 한계가 있습니다.
그래서 Attention 메커니즘은 '함축적으로 담긴 Context Vector에 의존하지 말고 기존 모든 token을 다 보자!'라는 아이디어를 제안합니다. token들을 보면서 Decoder에 들어가는 문장(번역할 문장)의 각 token에 대해서 Encoder의 각 token이 각각 얼마큼 중요한지 값을 매겨서 그걸 토대로 번역을 해보자는 겁니다. (token이라 적었지만 token에 해당하는 LSTM 셀의 hidden state를 의미합니다.)
여기까지 봤을 때는 아직 Attention이 무엇인지 감이 안 옵니다. 당연히 왜 Attention이 필요한지만 다루어 보았으니까요. 다음은 Convolutional mechanism의 문제점에 대해서 알아봅시다.
📄 Convolutional mechanism의 문제점
Convolutional mechanism의 문제점을 알아보기 위해서는 극단적인 예시가 하나 필요합니다. '새로운 물체'라는 것이 세상에 존재한다고 가정합시다. 그리고, '새로운 물체'라는 것은 이미지로 표현했을 때 아래와 같이 생긴 거죠. '뭔 소리야?' 하실 수도 있지만, 세상에 없는 물체를 가정하는 거죠. '좌상단 동그라미 하나, 우하단 동그라미 하나'가 '새로운 물체'라고 가정하는 겁니다.
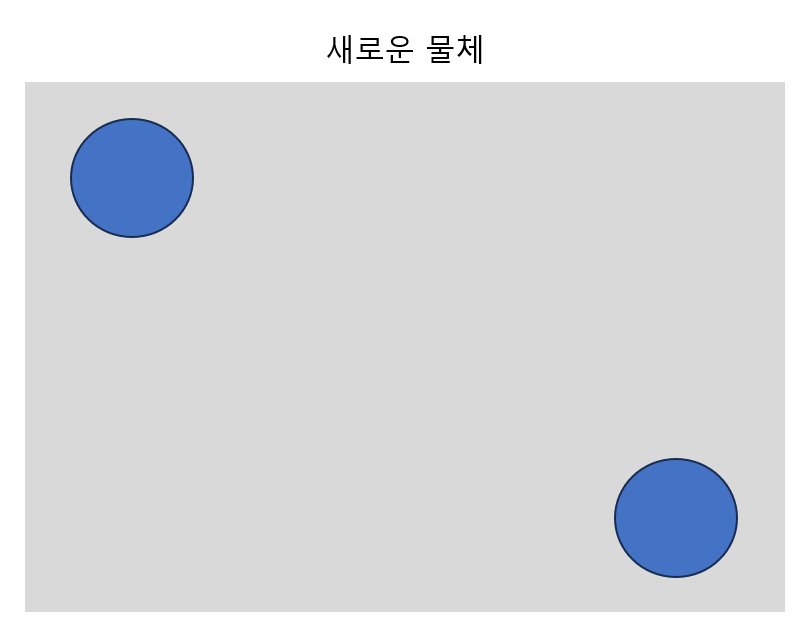
이 이미지를 사용해서 '새로운 물체'라는 것을 CNN을 통해 Classification 해봅시다.
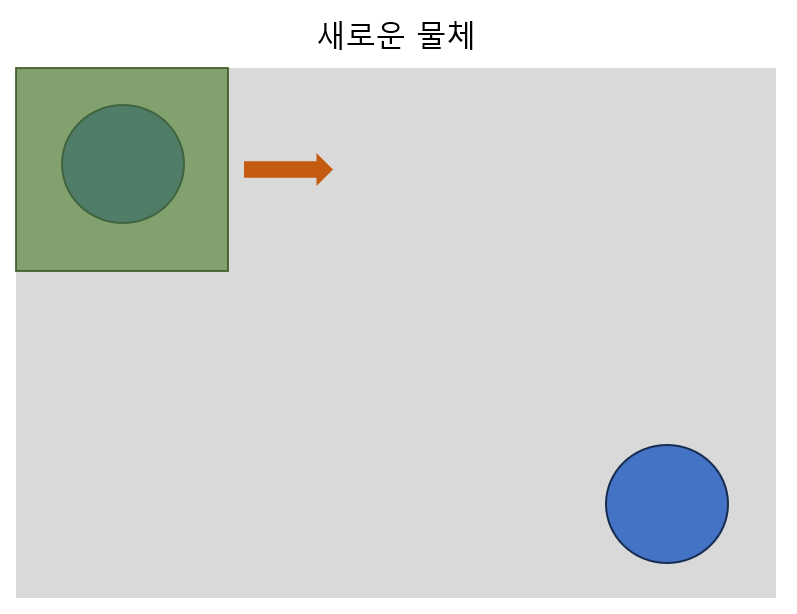
filter는 좌상단부터 시작해서 stride만큼의 간격으로 이동하면서 이미지의 부분들을 Convolution하여 결과를 도출할 것입니다. 하지만, 여기서 문제점은 좌상단의 동그라미와 우하단의 동그라미 사이의 위치적인 관계가 고려가 되나요?

CNN이라면 이것도 '새로운 물체'라고 분류를 할 수 있겠죠. 아님에도 불구하고 말입니다. filter가 스쳐가는 부분 이미지들에 대해 서로의 관계를 알아낼 수 있다면 좋지 않을까요? 좌상단 동그라미가 '나는 우하단에 동그라미가 있어야 '새로운 물체'야'라고 말할 수 있는 그런 위치적 관계성 말입니다. 위에서 말한 seq2seq에서 attention이 제안된 것처럼요.
비전 분야에서 attention을 적용하는 방법에 대해 설명하기 위해서는 ViT의 아이디어를 조금 설명해야 합니다. seq2seq에서는 문장이 token으로 나누어지고, 각 token을 embedding 하는 방식입니다. 그리고, attention을 적용하여 한 token에 대해 모든 token을 다 고려해 보는 것입니다.
ViT에서는 이런 방법을 착안하여 이미지를 동일한 크기 patch로 나눕니다.

그리고, 각 patch를 Embedding을 하여 Attention이 가능한 상태로 만드는 것입니다.

patch로 분할한 Embedding을 통해 이제 Recurrence mechanism과 똑같이 각 patch(= token in seq2seq)한테 모든 patch를 탐색하면서 어떤 patch가 지금 현재의 patch에게 중요한가를 고려할 수 있는 상태가 되었습니다.
이제는 좌상단 동그라미가 말할 수 있겠네요. '난 저 우하단에 뭐가 있는지 봐야해 동그라미가 있으면 그건 나한테 좀 중요해!'
📄 Attention을 들어가면서
이제 Attention이 왜 등장했는지 기존의 mechanism들의 문제점을 보면서 알게 되었습니다. 당연히 아직은 '어떻게' 돌아가는 mechanism인지는 어렵습니다. 다만, 문제점들을 말하면서 Attention mechanism의 핵심 키워드들을 언급했습니다.
'전체를 본다', '각 Embedding간의 관계성'
이 2가지 키워드를 가지고서 이제 Attention의 작동 원리를 알아봅시다.
✅ Attention (Query-Key-Value System)
(본 포스팅에서는 Scaled Dot-Product Attention을 기반으로 설명합니다.)
갑자기 'Query-Key-Value' 라는 키워드가 등장합니다. 데이터베이스를 다루어본 사람들은 무슨 개념인지 알 겁니다.
Query(요청)을 DB에 보내면 Key와 대조하면서 Query와 일치하는 Key라면 Value(데이터)를 가져오는 그런 체계입니다. 'DB 개념이 왜 나올까' 싶은데 공부를 해보니 이 개념만큼 비유가 적절한 개념은 없다는 걸 알았습니다.
하지만, 중요한 건 기존에 'Query-Key-Value'라는 체계를 알고 있다면, 이 것에 대해 너무 의존적으로 생각하지는 말아야 합니다. Attention에서는 살짝 더 모호한 개념이기 때문에 오히려 아예 모르는 상태에서 보는 것이 더 좋을 수 있습니다.
📄 Make 'Query-Key-Value'
처음에 Transformer, ViT 논문을 보면서 Attention에 대한 input을 봤을 때는 당황했습니다. 아래 그림을 보면, 3개의 input으로 들어가는데 이는 각각 Query, Key, Value를 의미합니다. 이러한 3가지 input에 대해서 '분할을 해야하나?, 그러면 안 될 거 같은데'라는 생각으로 의문을 품었습니다.

공부를 더 하다 보니 분할이 아니었음을 알게 되었습니다. Embedding을 각각 Query, Key, Value로 변환을 하는 체계였습니다. 변환은 Embedding에 대해 \(W_Q,W_K,W_V\) 행렬을 곱하여 \(Q,K,V\)만들어냅니다. 이때, \(W_Q,W_K,W_V\)는 trainable 하다는 특징을 가지고 있습니다. 당연히 최적의 \(Q,K,V\)를 만들어내기 위해서는 학습을 하면서 최적 값으로 맞춰가야 하기 때문입니다.
우선, Embedding이 어떻게 생겼는지 알아야 방금 말을 이해할 수 있습니다. 하나의 token이든 patch든 모두 Embedding을 하기 때문에 Embedding을 한 결과는 하나의 vector로 나타납니다. \(e_{n,m}\)은 n번째 Embedding의 m번째 Element입니다. 개념이 조금 복잡하기 때문에 편의를 위해서 하나의 Embedding을 \( [E_1] \)라고 표현하겠습니다.
$$ Embedding =
\begin{bmatrix}
e_{1,1}&e_{1,2}&\dotsm&e_{1,4}
\end{bmatrix}
= [E_1] $$
그러면 하나의 Input(Sentence, Image)은 Embedding 된다면, 이렇게 표현할 수 있겠네요.
$$ input =Embeddings =
\begin{bmatrix}
e_{1,1}&e_{1,2}&\dotsm&e_{1,m} \\
e_{2,1}&e_{2,2}&\dotsm&e_{2,m} \\
\vdots&\vdots&\ddots&\vdots \\
e_{n,1}&e_{n,2}&\dotsm&e_{n,m} \\
\end{bmatrix}
=
\begin{bmatrix}
E_{1} \\
E_{2} \\
\vdots \\
E_{n} \\
\end{bmatrix} $$
그러면, Query, Key, Value를 각각 구할 수 있습니다. 이때, \(W_Q,W_K,W_V\)은 크기가 모두 같습니다. 그리고, 행과 열의 길이에 대해 말하자면, 행(row)은 우선 행렬 곱을 위해서 하나의 Embedding의 길이와 같아야 합니다. 문제는 열(col)입니다. 단순한 Attention을 위해서는 상관이 없지만, Attention을 여러 Layer의 걸쳐 사용한다면 원래의 input shape로 유지되는 것이 좋았습니다. 그래서 특별한 경우가 아니라면 열(col) 또한 Embedding의 길이로 맞춰준다면, 추후에 Attention을 연산했을 때, 원래의 input과 같은 shape을 얻을 수 있습니다.
결론적으로, Query-Key-Value를 구하는 것을 수식으로 나타내면 아래와 같습니다.
이 단락을 끝내기 전, 정말 중요한 것은 Query, Key, Value 행렬을 구하였지만 각 row는 여전히 각 Embedding을 의미하고 있다는 것을 반드시 인지하고 있어야 합니다.
$$ \begin{align}
Query &=
\begin{bmatrix}
E_{1} \\
E_{2} \\
\vdots \\
E_{n} \\
\end{bmatrix}
\times
W_Q=Q=
\begin{bmatrix}
Q_{1} \\
Q_{2} \\
\vdots \\
Q_{n} \\
\end{bmatrix}
\\
Key &=
\begin{bmatrix}
E_{1} \\
E_{2} \\
\vdots \\
E_{n} \\
\end{bmatrix}
\times
W_K=K=
\begin{bmatrix}
K_{1} \\
K_{2} \\
\vdots \\
K_{n} \\
\end{bmatrix} \\
Value &=
\begin{bmatrix}
E_{1} \\
E_{2} \\
\vdots \\
E_{n} \\
\end{bmatrix}
\times
W_V=V=
\begin{bmatrix}
V_{1} \\
V_{2} \\
\vdots \\
V_{n} \\
\end{bmatrix}
\end{align} $$
📄 Attention Score (Query-Key)
기존의 mechanism의 문제점을 다루면서 Attention에 대한 키워드를 잠깐 소개했었습니다.
'전체를 본다', '각 Embedding 간의 관계성'
전부 이 단락에서 이루어지는 키워드입니다. 우선, Attention에 대한 수식을 잠깐 살펴봅시다.
$$ Attention = \text{softmax}(\frac{QK^T}{\sqrt{d_k}})V $$
수식이 좀 어렵게 느껴질 수도 있습니다. 우선 \( QK^T \)에 대해 알아봅시다.
바로 위에서 \(Q,K,V\)의 각 row는 여전히 Embedding을 의미한다고 했습니다. 이 의미를 가지고 \(QK^T\)가 가지는 의미를 보면, 아래와 같습니다.

여기서 연산의 결과는 어떻게 될까요? 모든 Query를 고려해 보기엔 어려우니 Query 1의 계산 결과만 한 번 봅시다.

\(QK^T\)의 첫 행을 보면 첫 번째 \(Q\)가 각 \(K\)에 대해 곱연산 한 값을 element로 가지고 있습니다. 이제야, 이 수식에서 거의 모든 퍼즐이 맞춰지기 시작합니다.
첫 번째 Query가 모든 Key에 대해 곱 연산을 수행하고 이 것을 첫 번째 행으로 가진다는 것은 첫 번째 행의 의미는 이렇게 해석할 수 있습니다.
'첫 번째 Query에 대한 모든 Key의 관계성을 분석한 값'
즉, 첫 번째 Query의 입장에서 각 Key, 다시 말해서 Embedding들이 어떠한 관계를 지니는가에 대한 값이라 볼 수 있습니다. 드디어 Attention의 개념에 접근하게 되었습니다! 조금씩 이해가 가기 시작하는 거죠!!
그래서 이 값들을 더 세밀하고 정확하게 표현하기 위해 아래의 변환을 통해 표현을 한 것입니다.
$$ QK^T\to\text{softmax}(\frac{QK^T}{\sqrt{d_k}}) $$
두 번째 Query도 보면 마찬가지로 '첫 번째 Query에 대한 모든 Key의 관계성을 분석한 값'이 되겠네요!

결론적으로, \( \text{softmax}(\frac{QK^T}{\sqrt{d_k}}) \)는 어느 한 Embedding에서 전체 Embedding을 보았을 때, 각 Embedding들이 얼마나 중요한가 or 연관이 있는가, 즉 가중치의 역할을 한다는 것입니다.
그래서 이 식을 Attention Score라고 부릅니다.
📄 Attention Value
이제 각 Embedding의 입장에서 모든 Embedding에 대한 Attention Score(Weight)를 구해보았습니다. 이제 마지막 단락입니다. 이것만 이해하면 새로운 mechanism을 알게 되는 거예요!
들어가기 앞서, 'DB에서 나온 Query-Key-Value 체계에 대해 알고 있는 상태라면, 이것에 대해 너무 의존적으로 생각하면 이해하는 데에 있어 혼란스럽다'라고 위해서 말했습니다. 왜냐하면, 이제 그 이유가 나오기 때문이에요.
지금까지 구한 Attention Value가 Weight의 역할을 하는 데에다가 곱하는 피연산자가 Value라면, 당연히 Value의 중심적으로 생각하게 될 것입니다. 저는 이게 Attention을 이해하는 데에 있어 가장 큰 방해 요소였습니다. 마지막 단락에서 이해를 돕고자 작은 힌트를 드린다면, Attention에 있어서 모든 중심은 Value가 아닌 Query에게 있습니다. ('모든 연산의 결과의 row는 Query 중심적으로 생각하라'라는 의미입니다.)
바로 계산을 해보고 이에 대해 해석을 해보는 것으로 마무리하겠습니다.
\(QK^T\)와 \(V\)를 연산해 봅시다. 루트 값을 나누어주고, softmax를 사용하는 것은 여기서는 중요하지 않으니 간단화를 위해 생략하겠습니다.
$$ \begin{bmatrix}
Q_1K_1 & Q_1K_2 & Q_1K_3 \\
Q_2K_1 & Q_2K_2 & Q_2K_3 \\
Q_3K_1 & Q_3K_2 & Q_3K_3 \\
\end{bmatrix}
\times
\begin{bmatrix}
V_1 \\
V_2 \\
V_3 \\
\end{bmatrix}
=
\begin{bmatrix}
Q_1K_1V_1 + Q_1K_2V_2 + Q_1K_3V_3 \\
Q_2K_1V_1 + Q_2K_2V_2 + Q_2K_3V_3 \\
Q_3K_1V_1 + Q_3K_2V_2 + Q_3K_3V_3 \\
\end{bmatrix} $$
이 수식이 이해하는 데에 있어서 가장 복잡했던 개념이었습니다. 최대한 간단하게 표현해 본 게 이 정도네요.
여기서는 어떤 해석을 할 수 있을까요? '모든 Key는 Value에 대응한다' 저는 이 정도의 해석까지만 가능했습니다. 이런 이유에서 DB의 Query-Key-Value라는 개념을 도입한 게 아닐까 싶기도 한 부분이었죠.
하지만, 지금은 그게 목적이 아닙니다. 우리는 아까 위에서 \(QK^T\)를 일종의 Weight로 보았고, 계속 언급하듯이 연산의 모든 결과는 Query를 중심적으로 생각하라는 말을 했었죠. 이 두 정보를 기반으로 수식을 다시 써보면 이렇게 쓸 수 있겠네요
여기서 \(w_{i, j}\)는 i번째 Query가 j번째 Key에 대한 곱연산으로 Attention Score(Weight)라 정의합니다.
$$ \begin{bmatrix}
Q_1K_1V_1 + Q_1K_2V_2 + Q_1K_3V_3 \\
Q_2K_1V_1 + Q_2K_2V_2 + Q_2K_3V_3 \\
Q_3K_1V_1 + Q_3K_2V_2 + Q_3K_3V_3 \\
\end{bmatrix}
=
\begin{bmatrix}
w_{1,1}V_1 + w_{1,2}V_2 + w_{1,3}V_3 \\
w_{2,1}V_1 + w_{2,2}V_2 + w_{2,3}V_3 \\
w_{3,1}V_1 + w_{3,2}V_2 + w_{3,3}V_3 \\
\end{bmatrix} $$
이제야 무언가가 좀 보이기 시작합니다. 각 행은 Query를 중심으로 생각하라 했었습니다. 첫 행은 첫 Query에 대해서 모든 Value들에 Weight를 곱하여 다 더한 Weighted Sum(가중합)입니다.
드디어 해석이 되네요! 각 Query는 Key를 통해서 Value에 대한 중요도를 정하였고, Query의 입장에서 Value의 정보를 중요도를 따지면서 모두 가져온 다음, 모두 더하면서 현재 Query에서 전체적인 정보를 가져올 수 있는 겁니다!
더 확실하게 봅시다. 이렇게 보면 어떨까요, 결과의 각 행이 Query라는 것은 각 행을 각 Embedding으로 봐도 무방합니다.
그러면, 각 Embedding은 다음 Layer로 가면서 이렇게 말할 수 있습니다.
"나 2번째 Embedding인데 내가 1~N까지 모든 Embedding을 다 만나보면서 나랑 얼마나 관계가 깊은지 알아냈어! 그리고 그런 관계들을 모두 다 합쳐서 보니까 나는 이런 새로운 정보를 만들어 낼 수 있더라!"
기존의 Embedding과 Attention을 통해 만들어진 Attention Value의 차이가 이제 보입니다.
즉, Attention을 통해 만들어진 Embedding은 주위의 모든 Embedding을 고려하면서 중요하고, 중요하지 않은 Embedding으로 결정하며, 이러한 중요도를 바탕으로 다 더하여 새로운 정보를 만들어냅니다. '중요한 것에 집중을 하겠다'라고 해서 Attention이라는 이름이 붙었습니다.
✅ Conclusion
1. Attention mechanism은 기존의 Recurrence mechanism, Convolutional mechanism의 문제점을 해결하는 새로운 mechanism이다.
2. 전체적인 정보를 고려한다.
3. 전체적인 정보에서 각 정보에 대해 가중치를 부여한다. 이를 위해 Query-Key-Value 체계가 도입되었다.
4. 이러한 모든 정보를 더하여 Token or Patch 등 하나의 정보에 모든 정보가 담기도록 한다.
✅ Outro
새로운 mechanism을 접하고, 이에 대해 공부를 해보자 하니 자료가 많이 없어서 저의 관점을 계속 만들어내야 했습니다. 그래서, Attention을 공부해보고 싶은 사람들을 대상으로 내 관점을 한 번 보여주고 싶다는 마음으로 '강의처럼 작성을 해봐야겠다!'라고 느꼈습니다.
이러한 부분에서 다른 사람들의 관점, 이상한 부분들에 대해서 서로 댓글을 통한 교류가 있다면 더 확실한 지식이 될 겁니다. 감사합니다 :)
✅ Reference
[3] An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale
'AI > Concepts' 카테고리의 다른 글
| RMS Normalization, ICS의 해결책은 re-scaling에 있다. (0) | 2024.03.13 |
|---|---|
| Entropy와 Gini Impurity에 대하여: Decision Tree는 어떻게 만들어질까, Classification (1) | 2023.07.27 |
| Label Encoding의 문제점 (with Chat GPT) (0) | 2023.07.20 |
| Precision과 Recall이 반비례 관계인 이유에 대한 고찰 (1) | 2023.06.17 |
| Transfer Learning(pre-training, fine-tuning)의 개념에 대하여 (Prologue) (0) | 2023.02.04 |




