| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- c++
- BFS
- tensorflow
- 가끔은_말로
- NEXT
- object detection
- 백트래킹
- 미래는_현재와_과거로
- dropout
- DP
- 알고리즘
- 다익스트라
- lazy propagation
- 문자열
- 2023
- 이분 탐색
- 세그먼트 트리
- 너비 우선 탐색
- 우선 순위 큐
- 조합론
- back propagation
- 회고록
- dfs
- 자바스크립트
- pytorch
- Overfitting
- 가끔은 말로
- 크루스칼
- 분할 정복
- 플로이드 와샬
- Today
- Total
Doby's Lab
[알고리즘] 백준 15650번: N과 M (2) (C++), Backtracking의 개념, DFS와의 차이 본문

(N과 M (1) 문제를 중심으로 설명하려 했으나 Backtracking과 DFS의 차이를 설명하기 위해 N과 M (2) 문제가 적합하다는 생각이 들었다.)
개념
백트래킹은 DFS를 응용하여 나온 알고리즘 같았다.
DFS에 대해서는 그래프 이론에 대한 문제를 풀기 시작할 때 제대로 다시 다루겠지만 간단히 정리하면 어떠한 그래프가 주어졌을 때, 시작 노드로부터 연결돼있는 모든 노드를 탐색해나가는 완전 탐색 알고리즘이다. 또한 노드끼리 연결되었는가도 따져보아야 하는데 다음에 다시 다루겠다.

이러한 그래프가 있다고 가정하자.

시작 노드가 1일 때, DFS는 모든 노드들을 다음과 같이 탐색해나간다.
백트래킹은 DFS에 어떠한 조건을 주어서 (조건이라고 해서 무조건 if문을 사용하지 않는다.)
원하는 부분만 탐색하도록 하는 알고리즘이다.
위 그래프에서 '수열을 출력하고 싶은데 시작 노드가 1이고, 3을 포함하지 않는다'라는 문제가 주어지면
DFS에 특정한 조건을 걸어서 3이 있는 노드로 갔을 경우에 다시 되돌아온다고 해서 백트래킹(backtracking)이다.
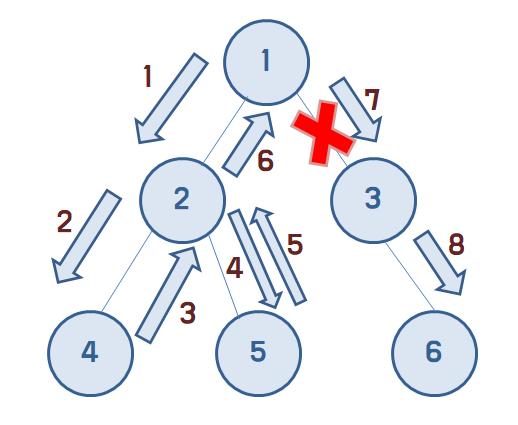
해당 그림에서는 3으로의 통로를 갔다가 돌아오게 되면서 6까지 도달하지 않지만 이건 개념을 위한 설명일 뿐이니 문제와 크게 관련 없다.
(문제에서는 모든 노드가 서로 간선(edge)을 갖고 있다고 생각하면 된다.)
저렇게 3으로 가는 통로를 끊어버리는 것같이 보이는데 이를 가지치기(pruning)이라고 한다.
3을 포함하는 것이 문제를 만족시키지 않기 때문에 '유망하지 않다'라고도 한다.
반대로 2로 가는 것은 정답을 만족시켜서 2의 노드는 '유망하다(promising)'이라 한다.
백트래킹과 DFS의 차이
정리를 해보자. 주관적으로 생각하기에는 백트래킹은 완전 탐색을 이용하는 DFS에서 특정한 조건을 걸어서 조건에 만족하는 일부 노드의 집합을 가져오는 알고리즘이라 생각한다.
즉, 일부만 가져온다는 점에서 시간 복잡도도 효율적으로 DFS보다 나올 것이다.
이론적으로 백트래킹과 DFS는 크게 연관이 없지만 문제를 보았을 때, DFS로 풀어야 하는 건가라는 생각이 들다가 백트래킹 알고리즘을 알고 나서 서로 유사한 점이 많다고 생각했다.
문제
백트래킹을 처음 접해서 다른 분의 코드를 참고했다.
https://cryptosalamander.tistory.com/55
[백준 / BOJ] - 15650번 N과 M(2) C++ 풀이
백준 - 단계별로 풀어보기 [15650] https://www.acmicpc.net/problem/15650 문제 풀이 dfs를 활용한 조합문제이다. 조합문제를 풀기 위해서는 간단하다. 재귀 호출에서, 현재 뽑은 원소의 이전값들은 고려하지.
cryptosalamander.tistory.com
#include <iostream>
#define MAX 9
using namespace std;
int n, m;
int arr[MAX] = { 0, };
bool visited[MAX] = { 0, };
void dfs(int num, int cnt)
{
if (cnt == m)
{
for (int i = 0; i < m; i++)
cout << arr[i] << ' ';
cout << '\n';
return;
}
for (int i = num; i <= n; i++)
{
if (!visited[i])
{
visited[i] = true;
arr[cnt] = i;
dfs(i + 1, cnt + 1);
visited[i] = false;
}
}
}
int main() {
cin >> n >> m;
dfs(1, 0);
}DFS 알고리즘이나 백트래킹이나 visited 배열을 사용하여 방문 여부를 파악하고 특히 재귀 호출(recursive call)을 한다는 점에서 많이 비슷하다고 느꼈다.
문제에서는 n과 m이 주어질 때, 1~n까지의 숫자에서 m개의 수를 골라 오름차순이 되는 부분 수열을 모두 출력하라 했는데 DFS를 사용할 경우 모든 부분 수열을 출력해서 예를 들어 n = 4이고, m = 3이면 '3, 2, 1'과 같은 조건을 만족하지 못하는 수열도 생긴다.
이를 해결하기 위해 num이라는 변수를 사용해서 조건을 만들어낸다.
>> num이 주어지고, num 보다 더 작은 수는 탐색하지 않는다.
특히 DFS나 백트래킹에서 제일 헷갈리는 부분이 재귀 호출과 재귀 호출 바로 밑에 있는 visited[i] = false; 부분이었다.
헷갈리지 않기 위해 시뮬레이션을 해보았다.
//main에서 dfs(1, 0)으로 시작
void dfs(int 1, int 0) // 1번째 dfs
{
if (0 == m)
{
for (int i = 0; i < m; i++)
cout << arr[i] << ' ';
cout << '\n';
return;
}
for (int i = 1; i <= 4; i++)
{
if (!visited[1])
{
visited[1] = true;
arr[0] = 1; // 현재 arr: 1
dfs(1 + 1, 1 + 1);
visited[1] = false;
}
}
}
void dfs(int 2, int 1) // 2번째 dfs
{
if (1 == m)
{
for (int i = 0; i < m; i++)
cout << arr[i] << ' ';
cout << '\n';
return;
}
for (int i = 2; i <= 4; i++)
{
if (!visited[2])
{
visited[2] = true;
arr[1] = 2; // 현재 arr: 1 2
dfs(2 + 1, 1 + 1);
visited[2] = false;
}
}
}
void dfs(int 3, int 2) // 3번째 dfs
{
if (2 == m)
{
for (int i = 0; i < m; i++)
cout << arr[i] << ' ';
cout << '\n';
return;
}
for (int i = 3; i <= 4; i++)
{
if (!visited[3])
{
visited[3] = true;
arr[2] = 3; // 현재 arr: 1 2 3
dfs(3 + 1, 2 + 1);
visited[3] = false;
}
}
}
void dfs(int 4, int 3) // 4번째 dfs
{
if (3 == m) // 이 조건에서 dfs가 종료되기 때문에 밑에 for문은 상관 없음
{
for (int i = 0; i < m; i++) // 출력
cout << arr[i] << ' ';
cout << '\n';
return; // 종료
}
for (int i = 4; i <= 4; i++) // 이 for문에 도달하지 않음
{
if (!visited[4])
{
visited[4] = true;
arr[3] = 4;
dfs(4 + 1, 3 + 1);
visited[4] = false;
}
}
}
// 여기서 한 번 출력: 1 2 3
// 중요
// 4번째 dfs가 종료되면 3번째 dfs의 for문으로 돌아가는데
// 이 때 visited[3] == false가 되고나서 다음 for문으로 간다는 사실을 인지해두어야 함
void dfs(int 3, int 2) // 3번째 dfs
{
if (2 == m)
{
for (int i = 0; i < m; i++)
cout << arr[i] << ' ';
cout << '\n';
return;
}
for (int i = 3; i <= 4; i++)
{
if (!visited[3])
{
visited[3] = true;
arr[2] = 3;
dfs(3 + 1, 2 + 1);
visited[3] = false; // <<< 이 부분 <<<
}
}
}
void dfs(int 3, int 2) // 3번째 dfs로 돌아가 남은 for문을 진행함
{
if (2 == m)
{
for (int i = 0; i < m; i++)
cout << arr[i] << ' ';
cout << '\n';
return;
}
for (int i = 4; i <= 4; i++)
{
if (!visited[4])
{
visited[4] = true;
arr[2] = 4; // 현재 arr: 1 2 4
dfs(4 + 1, 2 + 1); // i는 for 문에 의해 4가 되고, cnt는 3번째 dfs로 돌아왔기 때문에 계속 2이다.
visited[4] = false; // 4를 방문하지 않았다고 수정
}
}
}
void dfs(int 5, int 3) // 6번째 dfs
{
if (3 == m) // 이 조건에서 dfs가 종료되기 때문에 밑에 for문은 상관 없음
{
for (int i = 0; i < m; i++) // 출력
cout << arr[i] << ' ';
cout << '\n';
return; // 종료
}
// 밑에 for문을 보면 문법적으로 오류가 투성이다.
// 하지만 위의 조건문에 의해 for문까지 도달하지 않으므로 신경쓰지 않아도 된다.
for (int i = 5; i <= 4; i++) // 이 for문에 도달하지 않음
{
if (!visited[5])
{
visited[5] = true;
arr[3] = 5;
dfs(5 + 1, 3 + 1);
visited[5] = false;
}
}
}
// 여기서 한 번 출력: 1 2 4
// 이제 3번째 dfs까지 for문이 종료되어 2번째 dfs로 돌아간다.
// 2번째 dfs에서 i가 2일 때도 끝났으므로 visited[2] = false란 사실을 인지한다.
void dfs(int 2, int 1) // 2번째 dfs
{
if (1 == m)
{
for (int i = 0; i < m; i++)
cout << arr[i] << ' ';
cout << '\n';
return;
}
for (int i = 3; i <= 4; i++)
{
if (!visited[3])
{
visited[3] = true;
arr[1] = 3; // 현재 arr: 1 3
dfs(3 + 1, 1 + 1);
visited[3] = false;
}
}
}
void dfs(int 4, int 2) // 2번째 dfs
{
if (2 == m)
{
for (int i = 0; i < m; i++)
cout << arr[i] << ' ';
cout << '\n';
return;
}
for (int i = 4; i <= 4; i++)
{
if (!visited[4])
{
visited[4] = true;
arr[2] = 4; // 현재 arr: 1 3 4
dfs(4 + 1, 2 + 1);
visited[4] = false;
}
}
}
void dfs(int 5, int 3) // 7번째 dfs
{
if (3 == m) // 이 조건에서 dfs가 종료되기 때문에 밑에 for문은 상관 없음
{
for (int i = 0; i < m; i++) // 출력
cout << arr[i] << ' ';
cout << '\n';
return; // 종료
}
for (int i = 5; i <= 4; i++)
{
if (!visited[5])
{
visited[5] = true;
arr[3] = 5;
dfs(5 + 1, 3 + 1);
visited[5] = false;
}
}
}
// 여기서 한 번 출력: 1 3 4
// 다시 2번째 dfs로 돌아간다. 마지막 for문이었으므로 visited[4] == false를 넣고 끝낸다.
void dfs(int 4, int 2) // 2번째 dfs
{
if (2 == m)
{
for (int i = 0; i < m; i++)
cout << arr[i] << ' ';
cout << '\n';
return;
}
for (int i = 4; i <= 4; i++)
{
if (!visited[4])
{
visited[4] = true;
arr[2] = 4;
dfs(4 + 1, 2 + 1); // dfs(5, 3)을 끝내고 여기로 돌아와서
visited[4] = false; // 해당 문장을 수행하고 for문의 범위를 만족시켰으므로 2번째 dfs 종료
}
}
}
// 2번째 dfs가 종료된 후에 1번째 dfs로 돌아와서 visited[1] = false를 수행하고 다음 for문으로 넘어간다.
void dfs(int 1, int 0) // 1번째 dfs
{
if (0 == m)
{
for (int i = 0; i < m; i++)
cout << arr[i] << ' ';
cout << '\n';
return;
}
for (int i = 1; i <= 4; i++)
{
if (!visited[1])
{
visited[1] = true;
arr[0] = 1;
dfs(1 + 1, 1 + 1);
visited[1] = false; // << 이 부분 <<
}
}
}
void dfs(int 1, int 0) // 1번째 dfs
{
if (0 == m)
{
for (int i = 0; i < m; i++)
cout << arr[i] << ' ';
cout << '\n';
return;
}
for (int i = 2; i <= 4; i++)
{
if (!visited[2])
{
visited[2] = true;
arr[0] = 2; // 현재 arr: 2
dfs(2 + 1, 0 + 1);
visited[2] = false;
}
}
}
void dfs(int 3, int 1) // 8번째 dfs
{
if (1 == m)
{
for (int i = 0; i < m; i++)
cout << arr[i] << ' ';
cout << '\n';
return;
}
for (int i = 3; i <= 4; i++)
{
if (!visited[3])
{
visited[3] = true;
arr[1] = 3; // 현재 arr: 2 3
dfs(3 + 1, 1 + 1);
visited[3] = false;
}
}
}
void dfs(int 4, int 2) // 9번째 dfs
{
if (2 == m)
{
for (int i = 0; i < m; i++)
cout << arr[i] << ' ';
cout << '\n';
return;
}
for (int i = 4; i <= 4; i++)
{
if (!visited[4])
{
visited[4] = true;
arr[2] = 4; // 현재 arr: 2 3 4
dfs(4 + 1, 2 + 1);
visited[4] = false;
}
}
}
void dfs(int 5, int 3) // 10번째 dfs
{
if (3 == m) // 조건 만족
{
for (int i = 0; i < m; i++) // 출력
cout << arr[i] << ' ';
cout << '\n';
return; // 종료
}
// 밑에 for문을 보면 문법적으로 오류가 투성이다.
// 하지만 위의 조건문에 의해 for문까지 도달하지 않으므로 신경쓰지 않아도 된다.
for (int i = 5; i <= 4; i++)
{
if (!visited[5])
{
visited[5] = true;
arr[3] = 5;
dfs(5 + 1, 3 + 1);
visited[5] = false;
}
}
}
// 여기서 한 번 출력: 2 3 4
// 9번째 dfs로 돌아와서 visited[4] = false를 넣어두고, for문의 범위도 끝났으니 종료
void dfs(int 4, int 2) // 9번째 dfs
{
if (2 == m)
{
for (int i = 0; i < m; i++)
cout << arr[i] << ' ';
cout << '\n';
return;
}
for (int i = 4; i <= 4; i++)
{
if (!visited[4])
{
visited[4] = true;
arr[2] = 4; // 현재 arr: 2 3
dfs(4 + 1, 2 + 1);
visited[4] = false;
}
}
}
// 8번째 dfs로 돌아와서 마지막 for문을 수행함
void dfs(int 3, int 1) // 8번째 dfs
{
if (1 == m)
{
for (int i = 0; i < m; i++)
cout << arr[i] << ' ';
cout << '\n';
return;
}
for (int i = 4; i <= 4; i++)
{
if (!visited[4])
{
visited[4] = true;
arr[1] = 4; // 현재 arr: 2 3
dfs(4 + 1, 1 + 1);
visited[4] = false;
}
}
}
void dfs(int 5, int 2) // 11번째 dfs
{
if (2 == m)
{
for (int i = 0; i < m; i++)
cout << arr[i] << ' ';
cout << '\n';
return;
}
for (int i = 5; i <= 4; i++) // for문의 조건을 만족하지 않아서 for문을 지나치고 그대로 종료
{
if (!visited[5])
{
visited[5] = true;
arr[2] = 5; // 현재 arr: 2 3
dfs(5 + 1, 2 + 1);
visited[5] = false;
}
}
}
// 다시 8번째 dfs로 돌아가서 visited[4] = false를 넣고 for문까지 범위를 만족하여 1번째 dfs로 돌아간다.
void dfs(int 3, int 1) // 8번째 dfs
{
if (1 == m)
{
for (int i = 0; i < m; i++)
cout << arr[i] << ' ';
cout << '\n';
return;
}
for (int i = 4; i <= 4; i++) // << 범위 만족 <<
{
if (!visited[4])
{
visited[4] = true;
arr[1] = 4; // 현재 arr: 2 3
dfs(4 + 1, 1 + 1);
visited[4] = false; // << 이 부분 <<
}
}
}
// 1번째 dfs로 돌아와서 visited[2] = false를 수행한다.
void dfs(int 1, int 0) // 1번째 dfs
{
if (0 == m)
{
for (int i = 0; i < m; i++)
cout << arr[i] << ' ';
cout << '\n';
return;
}
for (int i = 2; i <= 4; i++)
{
if (!visited[2])
{
visited[2] = true;
arr[0] = 2; // 현재 arr: 2
dfs(2 + 1, 0 + 1);
visited[2] = false; // 이 부분을 수행하고 나서
}
}
}
// for의 i는 이제 3을 가리켜 남은 dfs를 수행해 나가겠지만
// 시뮬레이션은 여기서 끝내겠다.
// 상식적으로 1~4까지 수 중에 3부터 오름차순으로 3개를 나열할 수는 없다.
// 즉, 남은 dfs들은 11번째 dfs처럼 종료 될 것이다.
// 나온 출력들:
// 1 2 3
// 1 2 4
// 1 3 4
// 2 3 4느낀 점
- 새 알고리즘 백트래킹에 대해 알게 되었다.
- DFS와 백트래킹의 차이
- 시뮬레이션까지 해보았지만 백트래킹과 DFS에 대한 여러 문제를 통해 더 이해할 필요가 있다.
- 시뮬레이션 한번 더 했다간 성격 나빠지겠다.
참고
https://cryptosalamander.tistory.com/55
[백준 / BOJ] - 15650번 N과 M(2) C++ 풀이
백준 - 단계별로 풀어보기 [15650] https://www.acmicpc.net/problem/15650 문제 풀이 dfs를 활용한 조합문제이다. 조합문제를 풀기 위해서는 간단하다. 재귀 호출에서, 현재 뽑은 원소의 이전값들은 고려하지.
cryptosalamander.tistory.com
https://gamedevlog.tistory.com/49
백트래킹(back tracking)
Goal 백트래킹에 대해 설명할 수 있다. DFS와 백트래킹을 설명할 수 있다. 백트래킹(backtracking)이란? 솔루션을 찾는 과정에서, 유망(promising)하지 않은 후보해에 대해 대해 빠르게 포기하고 이전 단
gamedevlog.tistory.com
https://hongjw1938.tistory.com/88
알고리즘 - 백트래킹(Backtracking)
1. 백트래킹이란? 백트래킹은 알고리즘 기법 중 하나로, 재귀적으로 문제를 하나씩 풀어나가되 현재 재귀를 통해 확인 중인 상태(노드)가 제한 조건에 위배되는지(유망하지 않은지) 판단하고 그
hongjw1938.tistory.com
'PS > BOJ' 카테고리의 다른 글
| [자료구조] 백준 17298번: 오큰수 (C++), Monotonic Stack (단조로운 스택) (0) | 2021.09.22 |
|---|---|
| [알고리즘] 백준 15663번: N과 M (9) (C++), 도식화의 중요성 (0) | 2021.09.19 |
| [알고리즘] 백준 2110번: 공유기 설치 (C++), (low + 1 < high)라는 조건, 논리의 부족 (0) | 2021.09.14 |
| [알고리즘] 백준 2805번: 나무 자르기 (C++), 이분 탐색 (함수 없이 직접 구현) (0) | 2021.09.13 |
| [알고리즘] 백준 10816번: 숫자 카드 2 (C++), 이분 탐색(binary search) 개념, (upper_bound, lower_bound) (0) | 2021.09.11 |




