| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 플로이드 와샬
- 백트래킹
- lazy propagation
- 분할 정복
- 가끔은_말로
- 세그먼트 트리
- 회고록
- 자바스크립트
- 2023
- pytorch
- 알고리즘
- tensorflow
- back propagation
- object detection
- 다익스트라
- NEXT
- dfs
- 우선 순위 큐
- 이분 탐색
- 가끔은 말로
- BFS
- 문자열
- Overfitting
- DP
- 크루스칼
- c++
- 미래는_현재와_과거로
- dropout
- 너비 우선 탐색
- 조합론
- Today
- Total
Doby's Lab
[알고리즘] 백준 2110번: 공유기 설치 (C++), (low + 1 < high)라는 조건, 논리의 부족 본문
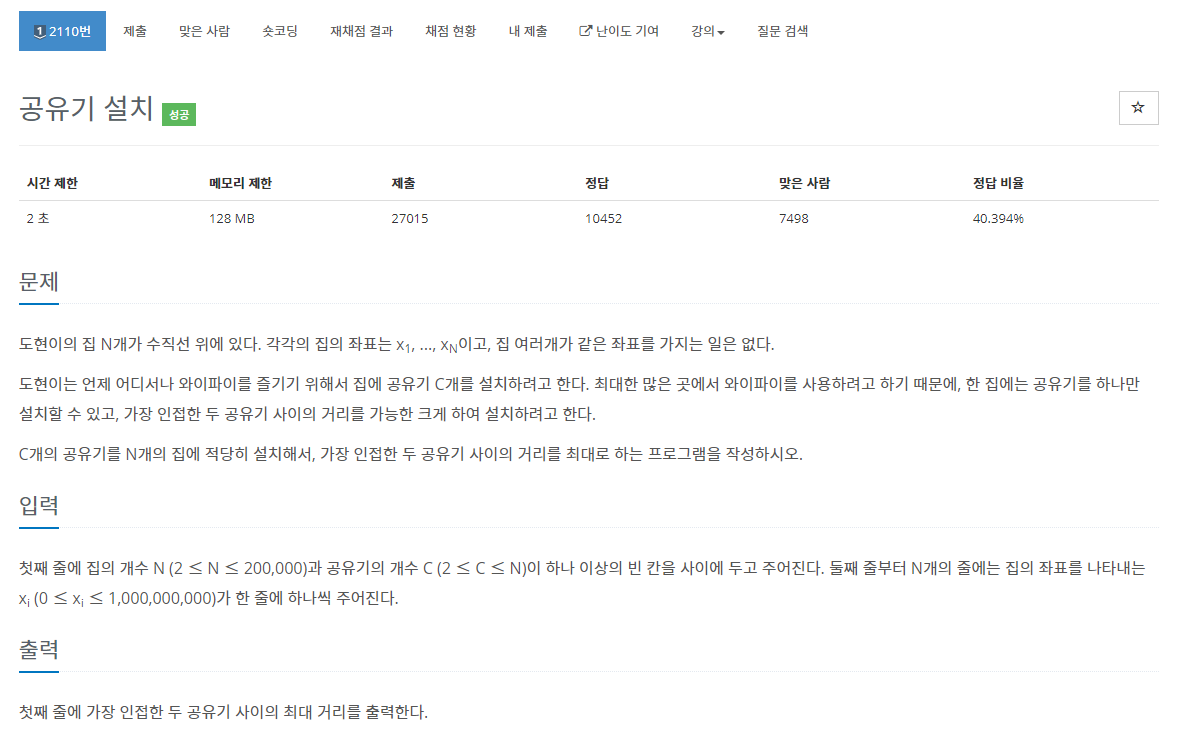
이 문제는 논리를 짤 수 없어서 다른 사람들의 답을 참고했다.
그래도 이분 탐색을 사용해서 풀어보고자 했던 마음이 있었기에 논리만 참고했다.
논리는 이랬다.
어떠한 거리가 주어지면 '그 거리와 같거나 그 이상의 거리를 가질 때'의 공유기가 설치될 수 있는 개수가 주어진 C보다 많으면 거리를 더 늘려서 탐색해나가고,
그와 반대로 어떠한 거리가 공유기가 설치될 수 있는 개수보다 작으면 거리를 좁혀서 탐색해나가는 논리였다.
논리를 알기 전까지는 어디에 포커스를 두어야 할지도 몰랐다.
구하는 것이 거리이기에 거리에 초점을 두어야 했을까
코드 탐색
내가 짠 코드를 토대로 나름의 해설을 해두어야 할 거 같다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main() {
int N, C;
cin >> N >> C;
//집의 좌표를 입력
vector<long long int> home;
for (int i = 0; i < N; i++) {
long long int a;
cin >> a;
home.push_back(a);
}
//집의 좌표를 오름차순으로 정렬
sort(home.begin(), home.end());
// 집 사이의 가질 수 있는 최소의 거리 = 1
long long int low = 1;
// 집 사이의 가질 수 있는 최대의 거리 = 맨 끝 - 맨 앞
long long int high = home.back() - home.front();
// while 안에 알고리즘
// (1): 논리
// 공유기가 설치된 집에서 직전에 설치된 집까지의 거리가 mid보다 크면 pass
// mid보다 작다면 다음 좌표로 넘어가서 mid를 만족할 때까지 넘어감
// (2): low와 high 기준
// 설치될 수 있는 공유기의 개수가 C보다 크거나 같은 경우 거리를 좀 더 늘려도 된다는 뜻이므로
// low = mid
// 반대로 작은 경우에 거리를 줄여서 설치해야 하는 공유기의 개수와 설치 될 수 있는 공유기의 개수를 맞춰야 하므로
// low = high
long long int answer = 0;
while (low <= high) {
long long int mid = (low + high) / 2;
int beforeIdx = 0;
int installPossible = 1; // 애초에 하나는 설치가 되어있다 0으로 할당을 해서 논리에 오류가 있음을 알았다.
for (int i = 0; i < home.size(); i++) {
if (home[i] - home[beforeIdx] >= mid) {
beforeIdx = i;
installPossible++;
}
}
//cout << installPossible << ' ' << mid << " " << low << ' ' << high << '\n';
if (installPossible >= C) {// 같을 때는 거리의 최댓값을 구하기 때문에 범위를 더 높혀서 탐색한다.
low = mid + 1;
answer = mid;
}
else {
high = mid - 1;
}
}
cout << answer;
return 0;
}1. 집의 좌표를 순서대로 배치된 상태에서 탐색해야 했기에 정렬을 해주었다.
2. 설치 가능한 수(installPossible)가 1이 되어야 한다.
처음에는 0으로 설정해두어서 이상하게 1이 빠진 값들이 출력됐었는데 맨 앞에 있는 집에 설치를 해두고서 시작을 해야(초기값을 1로 잡아야) 논리가 가능하기 때문이다.
3. 이 때까지는 이분 탐색의 조건을 항상 low + 1 < high로 두었었다.
(low + 1 < high)와 (low <= high)를 두고서 이 문제에서 한 번 시도를 해봤다.
이때까지 low + 1 < high를 사용했었는데 왜냐하면 이는 mid를 담아내는 low에서 바로 출력이 가능했기 때문이다.
단지 이것이 편하다는 생각이었고, 이 문제에서 low = mid + 1을 할당하기에 따로 answer 변수를 선언해주어야 했다.
answer에 mid를 할당하는 변수를 선언했다.
low = mid + 1이 되고, high = mid - 1이 되는 이유는 사실 이게 더 효율적인 면이 있다.
범위를 기존보다 더 최적화시키기 때문이다. (mid보다 큰 값 or mid보다 작은 값)
그리고 이 때문에 조건이 low <= high가 되는데
이것은 예를 들어 low = mid + 1인데 high와 같아지거나 더 커지면 이분 탐색이 끝나야 하기 때문이다.
그리고 앞으로 low <= high를 사용해야겠다고 생각한 결정적인 이유는
조건이 low + 1 < high일 때 이분 탐색은 3번 일어났지만 low <= high일 때 4번으로 확실히 끝내는 듯한 느낌이 있었기 때문이다.
결론
1. 이번 문제는 논리에 접근을 할 수 없었다. 논리에 접근하는 능력을 키울 수 없을까
2. 이분 탐색 while의 조건을 (low + 1 < high)에서 (low <= high)를 사용하고 결괏값을 담아내는 변수를 하나 선언해서 사용해야겠다.
'PS > BOJ' 카테고리의 다른 글
| [알고리즘] 백준 15663번: N과 M (9) (C++), 도식화의 중요성 (0) | 2021.09.19 |
|---|---|
| [알고리즘] 백준 15650번: N과 M (2) (C++), Backtracking의 개념, DFS와의 차이 (0) | 2021.09.16 |
| [알고리즘] 백준 2805번: 나무 자르기 (C++), 이분 탐색 (함수 없이 직접 구현) (0) | 2021.09.13 |
| [알고리즘] 백준 10816번: 숫자 카드 2 (C++), 이분 탐색(binary search) 개념, (upper_bound, lower_bound) (0) | 2021.09.11 |
| [알고리즘] 백준 1929번: 소수 구하기 (C++), 에라토스테네스의 체 (0) | 2021.09.08 |




