| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- DP
- dfs
- 이분 탐색
- 회고록
- back propagation
- tensorflow
- 2023
- 플로이드 와샬
- Overfitting
- 가끔은_말로
- pytorch
- BFS
- 가끔은 말로
- 세그먼트 트리
- dropout
- 조합론
- 우선 순위 큐
- c++
- 너비 우선 탐색
- 크루스칼
- 문자열
- 알고리즘
- lazy propagation
- 백트래킹
- NEXT
- 자바스크립트
- 다익스트라
- 미래는_현재와_과거로
- 분할 정복
- object detection
- Today
- Total
Doby's Lab
[알고리즘] 백준 2096번: 내려가기 (C++), 블로그는 지적 재산이라는 명제는 참이다. 본문
https://www.acmicpc.net/problem/2096
2096번: 내려가기
첫째 줄에 N(1 ≤ N ≤ 100,000)이 주어진다. 다음 N개의 줄에는 숫자가 세 개씩 주어진다. 숫자는 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 중의 하나가 된다.
www.acmicpc.net
이번 문제는 블로그 활동에 대해 성취감을 주는 문제였다.
>> 최근 들어 블로그에 정리해둔 내용들을 직접 써먹는(?) 기회들이 많았다.
1) 우선 3개의 열을 가진 배열을 사용하여 DP를 돌려야겠다는 생각은 다음 문제들로부터 영감을 얻었다.
(1. 1309번 정리 https://draw-code-boy.tistory.com/87)
(2. 2249번 정리 https://draw-code-boy.tistory.com/51)
2) 메모리를 보면 4MB로 10000의 행을 가진 2차원 배열을 선언하기에는 턱없이 부족한 메모리다.
>> 즉각적으로 DP를 처리하는 방법이 필요하다는 영감은 다음 문제에서 영감을 받았다.
(1. 4150번 정리 https://draw-code-boy.tistory.com/77)
입력을 받는 대로 즉각적으로 DP를 처리해야 한다.
하지만, 조금의 논리력(?)이 필요하다.
다음은 최댓값을 구하는 코드다.
temp 변수를 사용해야겠다는 생각을 할 수 있는 게 이번 문제의 포인트다.
tempZero = maxdp[0]; tempTwo = maxdp[2];
maxdp[0] = max(maxdp[0], maxdp[1]) + input[0];
maxdp[2] = max(maxdp[2], maxdp[1]) + input[2];
maxdp[1] = max(max(tempTwo, maxdp[1]), tempZero) + input[1];왜 temp변수를 사용해야 하나?
그림으로 알아보자.
temp가 없이 maxdp[0]과 maxdp[2]를 사용한다면
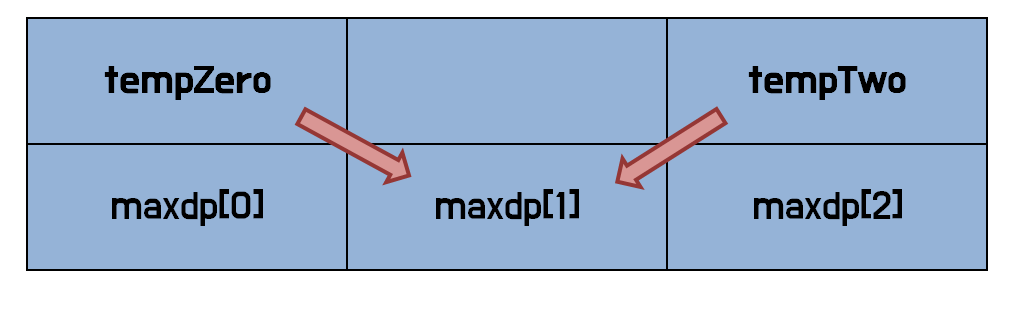
maxdp[0]와 maxdp[2]는 이미 내려온 값이다. 즉, 이전의 값을 담아야 하는데 즉각적인 처리 때문에 이전의 값을 기억할 수 있는 방법이 없기 때문에 temp변수에 이전의 값을 담아두는 것이다.
Q: 그럼 maxdp[1]을 구하는 코드를 맨 위로 올려놓으면 되지 않느냐?
A: 그건 다음 maxdp[0]과 maxdp[2]를 구할 때 똑같은 문제로 되돌아온다.
최솟값을 구하는 것도 똑같은 과정을 겪는다.
[AC 코드]
#include <iostream>
using namespace std;
int input[3] = { 0, };
int maxdp[3] = { 0, };
int mindp[3] = { 0, };
int tempZero, tempTwo;
int main() {
int n;
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> input[0] >> input[1] >> input[2];
tempZero = maxdp[0]; tempTwo = maxdp[2];
maxdp[0] = max(maxdp[0], maxdp[1]) + input[0];
maxdp[2] = max(maxdp[2], maxdp[1]) + input[2];
maxdp[1] = max(max(tempTwo, maxdp[1]), tempZero) + input[1];
tempZero = mindp[0]; tempTwo = mindp[2];
mindp[0] = min(mindp[0], mindp[1]) + input[0];
mindp[2] = min(mindp[2], mindp[1]) + input[2];
mindp[1] = min(min(tempTwo, mindp[1]), tempZero) + input[1];
}
cout << max(max(maxdp[2], maxdp[1]), maxdp[0]) << ' ';
cout << min(min(mindp[2], mindp[1]), mindp[0]);
return 0;
}느낀 점
예전에 어려웠던 문제나 애매했던 문제들을 정리해둔 걸 한 번에 많이 써먹었다. 너무 뿌듯하다.
'PS > BOJ' 카테고리의 다른 글
| [알고리즘] 백준 5073번: 삼각형과 세 변 (C++), 조건의 위치 (0) | 2021.11.12 |
|---|---|
| [알고리즘] 백준 9019번: DSLR (C++), 간결한 생각 (최적화) (0) | 2021.11.12 |
| [알고리즘] 백준 1309번: 동물원 (C++), 너무 아쉽다 (0) | 2021.11.12 |
| [알고리즘] 백준 11054번: 가장 긴 바이토닉 부분 수열 (C++), 메모이제이션 2번 (0) | 2021.11.12 |
| [알고리즘] 백준 11053번: 가장 긴 증가하는 부분 수열 (C++), 첫 LIS (0) | 2021.11.12 |

