| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 분할 정복
- object detection
- 다익스트라
- NEXT
- 플로이드 와샬
- 회고록
- 미래는_현재와_과거로
- 2023
- tensorflow
- lazy propagation
- 너비 우선 탐색
- BFS
- 세그먼트 트리
- dfs
- 가끔은_말로
- Overfitting
- 알고리즘
- 가끔은 말로
- 우선 순위 큐
- back propagation
- 조합론
- 이분 탐색
- pytorch
- 크루스칼
- 문자열
- dropout
- c++
- 자바스크립트
- 백트래킹
- DP
- Today
- Total
Doby's Lab
[알고리즘] 백준 2407번: 조합 (C++), Combination, Permutation 본문
https://www.acmicpc.net/problem/2407
2407번: 조합
n과 m이 주어진다. (5 ≤ n ≤ 100, 5 ≤ m ≤ 100, m ≤ n)
www.acmicpc.net
이번 문제는 (https://jaimemin.tistory.com/682)을 참고한다.
개념
학생 때 배웠던 nCr 개념이 등장한다. 정확히는 n Combination r이라고 부른다.
이와 같이 따라오는 게 nPr로 이는 n Permutation r이라고 부른다.
이 둘은 조합론으로 둘 다 공식이 존재한다.
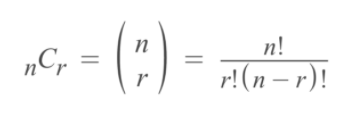

솔루션 1 (실패)
이 공식을 활용하여 두 개의 팩토리얼 함수를 구현하여 풀려고 했다.
[조금 다른 방식의 팩토리얼 함수]
각각 n!, (n - r)!, r! 은 시간이 오래 걸릴뿐더러 숫자까지 너무 커질 거라고 생각했다.
그래서 (n - r)!과 r! 중에 큰 값을 골라서 예를 들어 7C4를 구한다고 치면 7! / (3! * 4!)으로 7! 에서 4!으로 나누어 7 * 6 * 5까지만 곱하면 되기 때문에 시간을 줄일 수 있다고 생각했다. 거기다가 r! 을 곱하여 원하는 결괏값을 얻으려 했지만 시간 초과가 나고 만다.
솔루션 2 (참고)
떠올랐던 방법 말고는 떠오르는 방법이 없어서 참고를 해야 했다.
https://jaimemin.tistory.com/682
백준 2407번 조합
문제 링크입니다: https://www.acmicpc.net/problem/2407 백준 1793번 타일링(http://jaimemin.tistory.com/618)처럼 long long 자료형의 범위를 벗어나는 답을 구해야하기 때문에 string을 통해 Big Integer를..
jaimemin.tistory.com
이곳에서는 3가지의 포인트를 발견할 수 있었다.
- nCr = (n - 1)C(r - 1) + (n - 1)Cr 공식
- 너무 큰 수가 나오는 걸 방지하기 위한 문자열 변환 합 사용
- 시간 초과 방지를 위한 &(참조 연산자) 사용
1) nCr = (n - 1)C(r - 1) + (n - 1)Cr 공식
기존의 방식으로는 팩토리얼의 큰 값이 들어와서 부담스러웠는데 이 공식을 보고서 탑 다운 DP를 사용해서 풀 수 있겠구나를 알았다.
2) 너무 큰 수가 나오는 걸 방지하기 위한 문자열 변환 합 사용
C++이기 때문에 Biginteger가 따로 없어서 직접 선언해줘야 한다.
3) 시간 초과 방지를 위한 &(참조 연산자) 사용
이상하게 참고 자료를 분석 후, 구현했지만 시간 초과가 났었다. 차이는 &의 유무였다.
여기서 &(앰퍼샌드)는 주소 연산자가 아닌 참조 변수로 쓰인다.
>> 곧바로 포스팅 예정
(+ 2021.11.26 추가 내용)
https://draw-code-boy.tistory.com/103
[C++] 참조자(&)에 대하여, 포인터와는 전혀 다른 개념
https://draw-code-boy.tistory.com/101 [알고리즘] 백준 2407번: 조합 (C++), Combination, Permutation https://www.acmicpc.net/problem/2407 2407번: 조합 n과 m이 주어진다. (5 ≤ n ≤ 100, 5 ≤ m ≤ 1..
draw-code-boy.tistory.com
(2021.11.19 추가내용)
굳이 참조 변수를 쓸 필요는 없음
>> 참고하면서 바로 cache를 리턴할 생각을 못 했던 거 같다
string combination(int n, int r) {
if (n == r || r == 0) { // 0! = 1 이라는 성질
return "1";
}
//string& result = cache[n][r]; // 주소 변수 사용
if (cache[n][r] != "") {
return cache[n][r];
}
else {
return cache[n][r] = strSum(combination(n - 1, r - 1), combination(n - 1, r));
}
}
[AC 코드]
#include <iostream>
#include <cmath>
#include <algorithm>
#include <string>
using namespace std;
#define MAX 100 + 1
string cache[MAX][MAX];
string strSum(string a, string b) {
reverse(a.begin(), a.end());
reverse(b.begin(), b.end());
while (a.size() > b.size()) {
b += '0';
}
while (a.size() < b.size()) {
a += '0';
}
string result;
int carry = 0;
int alone;
for (int i = 0; i < a.size(); i++) {
alone = (a[i] - '0') + (b[i] - '0') + carry;
result += (alone % 10) + '0';
carry = alone / 10;
}
if (carry != 0) {
result += to_string(carry);
}
reverse(result.begin(), result.end());
return result;
}
string combination(int n, int r) {
if (n == r || r == 0) { // 0! = 1 이라는 성질
return "1";
}
string &result = cache[n][r]; // 주소 변수 사용
if (result != "") {
return result;
}
else {
return result = strSum(combination(n - 1, r - 1), combination(n - 1, r));
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int n, m;
cin >> n >> m;
cout << combination(n, m);
return 0;
}
'PS > BOJ' 카테고리의 다른 글
| [알고리즘] 백준 2206번: 벽 부수고 이동하기 (C++), 새로운 유형 BFS + Greedy (0) | 2021.11.20 |
|---|---|
| [알고리즘] 백준 14562번: 태권왕 (C++), 범위 오류 (0) | 2021.11.19 |
| [알고리즘] 백준 9465번: 스티커 (C++), 논리와 직관 그 어디쯤 사이에 (1) | 2021.11.18 |
| [알고리즘] 백준 1107번: 리모컨 (C++), 모든 경우의 수 (0) | 2021.11.17 |
| [알고리즘] 백준 11725번: 트리의 부모 찾기 (C++), 2차원 동적 배열 (vector) (0) | 2021.11.17 |


