| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 분할 정복
- 알고리즘
- 플로이드 와샬
- NEXT
- BFS
- 가끔은 말로
- dropout
- 이분 탐색
- 회고록
- back propagation
- 가끔은_말로
- pytorch
- 문자열
- tensorflow
- 크루스칼
- 자바스크립트
- object detection
- 조합론
- 다익스트라
- 세그먼트 트리
- Overfitting
- dfs
- 너비 우선 탐색
- 우선 순위 큐
- DP
- 2023
- c++
- 미래는_현재와_과거로
- 백트래킹
- lazy propagation
- Today
- Total
Doby's Lab
[알고리즘] 백준 4307번: 개미 (C++) 본문

이번 문제는 답을 구하고 싶었다. 무조건... (어떤 미래가 기다리고 있는지도 모른 채로...)
지금 현재 주어진 상황 (개인적인 얘기)
문제에 대해 들어가기 전에 현재 웃픈 상황에 대해 설명하고 싶다.
어제 서점을 들렸다가 읽어보고 싶은 책이 있어서 찾고 나서 서론을 봤는데(이코 테: 나동빈 님 책) 의외로 코딩 테스트에서 구현과 문자열의 비중이 상당히 높은 걸 알 수 있었다.
'시간을 내서 '구현' 문제에 집중을 해봐야겠다'라는 생각을 했다. 왜냐하면 그 비중을 나타낸 그래프를 본 순간, '어쩌면 알고리즘 지식, 알고리즘 구현 능력만 가지고서 계속 문제를 풀었던 게 아닐까?', '흔히 말하는 '빡구현', 알고리즘 지식을 제외한 아이디어를 능력치로 친다면 난 아직 바닥이 아닌가?'라고 생각했기에 지금 처음 구현으로 고른 문제가 하필이면...
그래서 이번 문제는 물어놓고 놓지 않으려고, 발버둥을 쳤다. (물론 아주 좋은 태도라고 생각하지만)
평소에는 엄청난 복잡함을 요구하는 문제라면 '이런 솔루션이 아니라 더 간단한 솔루션이 있을 거 같다', '실버에 이런 문제가 나온다고? (티어를 따져서 문제를 푼다는 게 좋은 생각은 아닌 듯)' 생각하며 내 솔루션이 틀렸음을 인정하고 다른 솔루션을 떠올리거나 구글링을 한다.
하필이면 이 문제에서 높은 이상의 복잡함을 느꼈음에도 '그래 이게 구현이지!!... 그래...' 하고 계속 풀려다가 그래 이건 아니다 인정하고 답 코드의 길이를 본 순간 밀려오는 상실감은... 어우
하지만, 이 마저도 답 코드를 구현하는 데에 있어서 논리는 이해할 수가 없었다. 스스로 풀던 코드에 영향을 받은 게 틀림없다. ('이 경우는 왜 안 따져?', '이게 말이 돼?' 혼잣말 많이 했다^^)
솔루션
(+참고 https://jaimemin.tistory.com/1178)
(+참고 2 (결정적으로 많이 도움됨 https://blog.naver.com/omi7894/222028279828))
(+애드혹(Ad-Hoc) 개념 참고 https://ndb796.tistory.com/474)
알고리즘 분류에 '애드혹'으로 분류되어 있길래 찾아봤더니 '정교한 알고리즘이 아닌 아이디어에 의존', '창의력에 의존'과 비슷한 말이라고 생각할 수 있었다. (구현 유형, 그리디 유형, 수학 유형이 이에 해당된다고 한다.) 가져온 이유는 '내 창의력이 아직은 바닥이다'라는 걸 세게 한 번 느끼려고...
참고한 링크를 보면 '두 개미가 만났을 때, 방향을 바꾸어 걸어가야 한다는 것은 전혀 고려하지 않아도 된다'라는 말은 그게 되려나 싶어서 논리를 보았다.
이 논리가 통하는 걸 직접 두 눈으로 보고 싶어서 '정말 이게 말이 되나'싶은 예시를 가져왔다.
우선 2마리인 경우는 수가 적고 직관적으로 확인할 수 있어서 이해는 쉬웠으나 이것이 3마리가 될 때도 통한다는 게 이해가 되지 않아서 시뮬레이션을 해보았다
[2마리의 경우]

논리에 따르면 각 점(시작점 혹은 끝점)에서 제일 멀리 떨어진 첫 번째 개미가 오른쪽으로 가는 경우에 최대 시간이 발생한다.
하지만, 부딪히는 것을 고려해야 하므로 부딪히는 것을 시뮬레이션해보면

파란색 화살표처럼 같은 거리만큼 가서 부딪힌다. (개미의 속도는 모두 똑같으니까)

부딪히고 나서 서로 다른 방향으로 가게 된다.
이때 첫 번째 개미는 거리가 짧아 먼저 떨어지게 되고, 두 번째 개미가 더 많은 거리가 남아서 두 번째 개미의 시간이 최대 시간이 된다.
두 번째 개미의 거리를 계산해보면
아까 부딪히기 전까지 움직인 거리가 첫 번째 개미가 움직인 거리가 똑같아서
두 개미가 모두 오른쪽 방향으로 가든 부딪히든 거리가 똑같다는 것을 알 수 있다.
하지만 '이것이 3마리인 경우에도 가능한가'가 나의 제일 궁금한 점이었다.
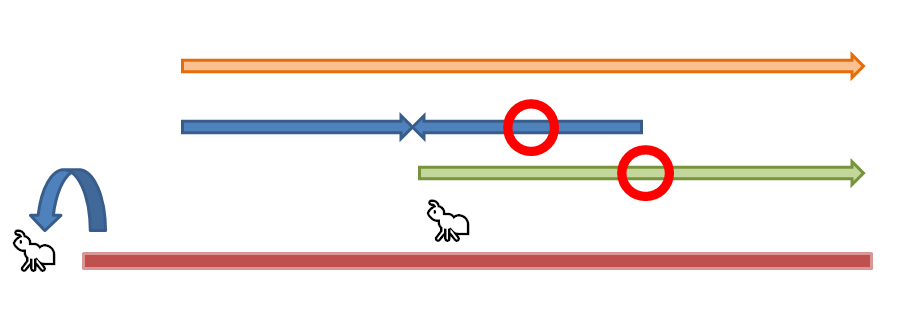
[개미가 3마리인 경우]

다음과 같이 막대에 3마리가 있다. 논리대로라면 1번 개미가 오른쪽으로 가는 경우(막대의 길이 - 1번 개미의 위치)가 최대 시간이 된다.

보이다시피 2번 개미, 3번 개미를 고려하더라도 1번 개미가 오른쪽으로 가는 데에 걸리는 시간이 최대 시간임을 알 수 있다.
3마리에서 부딪히는 경우들이 허용될까 싶어서 시뮬레이션을 돌리는 것이기 때문에 최대한 많이 부딪히게 해 보기 위해
1번 개미는 오른쪽, 나머지는 다 왼쪽 방향으로 가게 했다.

파란색 화살표만큼 가서 부딪히게 된다. 3번 개미에게도 시간이 흐르니 똑같은 거리만큼 간다.

충돌이 일어난 후, 1번 개미는 방향을 바꿔 추락을 하게 된다.
이제 2번 개미와 3번 개미가 충돌할 차례다. (이렇게 보니 2마리인 경우와 왜 다를 바가 없는지 알겠다.)

2번 개미와 3번 개미가 충돌한 후, 3번 개미는 오른쪽 방향, 2번 개미는 왼쪽 방향으로 가게 된다.
거리상으로는 2번 개미가 더 짧기 때문에 2번 개미가 먼저 떨어지게 된다.
그래서 3번 개미에게 걸린 시간이 최대 시간이 된다.
3번 개미가 간 거리는 1번 개미가 부딪히는 것을 고려하지 않고, 오른쪽이 가는 시간과 똑같음을 알 수 있다.

이쯤에서 헷갈릴까 봐 한 번 더 언급해야 할 것은 '2번 개미가 가는 거리가 최대일 수도 있지 않느냐?'라는 반박이다.
내가 이 부분에서 엄청나게 시간을 잡아먹었기 때문이다.
즉, 이것이 무슨 말이냐면 "3마리인 경우를 따질 때 맨 위에서 1번 개미가 최댓값을 가질 것이다."라고 했다.
이건 2마리인 경우로 반박에 대한 답을 줄 수 있다.

2마리인 경우에서 사용한 그림을 그대로 가져왔다. 반박하고자 하는 내용을 보자면 '1번 개미가 뛰어내기 직전까지의 걸린 시간이 최대가 될 수도 있지 않느냐'인데

2번 개미의 거리는 파란색 + 보라색인데 파란색 + 초록색보다 작은 것을 알 수 있다.
어찌 되던 '1, 2, 3번 개미들 중 2번 개미가 마지막으로 나와서 그것이 다른 최댓값을 유발할 수 있지 않느냐?'가 내가 가장 궁금한 점이었는데 그렇게 될 경우도 1번 개미에게 바통터치가 되어 1번 개미에서 최댓값을 구하는 것과 같다는 걸 알 수 있었다.
즉, 최솟값은 각 점(시작점 혹은 끝점)으로부터 가장 멀리 있는 개미가 나오는 시간
최댓값은 각 점으로부터 가장 가까이 있되 그것의 반대 방향으로 가는 데에 걸린 시간이다.
다음을 코드로 나타내면
사실 코드에서도 '다른 개미의 경우는 안 따지냐' 하지만 따지고 있다. 다만, 코드를 짜기 전 논리에서 최댓값이 어떻게 나오는 건지 확인이 되었을 뿐이다.
#include <iostream>
#include <cmath>
using namespace std;
int main() {
int T;
cin >> T;
for (int i = 0; i < T; i++) {
int length, n;
cin >> length >> n;
int minTime = 0, maxTime = 0;
for (int j = 0; j < n; j++) {
int ant;
cin >> ant;
int antMin = min(ant, length - ant);
int antMax = max(ant, length - ant);
minTime = max(minTime, antMin);
maxTime = max(maxTime, antMax);
}
cout << minTime << ' ' << maxTime << '\n';
}
return 0;
}느낀 점
이번 문제는 논리가 정말 어려웠다. 애초에 이 문제에 이러한 규칙이 있을 거라고는 상상을 못 했다.
최댓값을 구하는 과정에서 이건 '바통 터치'같다는 생각을 하기도 했다.
그리고, 제일 시간을 많이 잡아먹었던 건 예외의 경우가 통하는가? 였다.
최댓값이 그렇게 구해지는 거라면 이 경우가 최댓값이 명확히 될 수 없는가를 직접 두 눈으로 봐야 이해를 90%에서 100%로 올릴 수 있었다.
그리고, 이번 문제를 풀면서 알게 된 애드혹(Ad-Hoc)의 존재가 '아직 갈 길이 멀구나'라는 걸 두리뭉실한 생각에서 확신시켜줬다.
내 코드.. (기록용 오답)
답에 접근한 코드도 아니고, 실행되는 코드도 아니지만 나중에 내 글을 내가 볼 때, '이랬구나...'라는 생각을 해보고 싶어서
[떠올린 논리]
틀렸지만 어떤 논리(솔루션)이 떠올랐었는지 적어두고 싶다.
최솟값을 구하는 건 쉬웠고, 최댓값이 문제였다.
부딪히는 걸 고려해서 맨 가운데에 있는 개미가 제일 많이 시간을 잡아먹을 거라고 생각했다.
그래서 개미의 수(N)가 홀수일 때와 짝수일 때를 나누어서 특정한 개미를 고르려고 했다.
짝수일 때는 중간에 위치한 두 개미 중 시간을 더 잡아먹는 개미를 골랐다.
(왼쪽에 위치한 개미는 시작점과의 거리를 재서 얼마나 더 잡아먹을지, 오른쪽에 위한 개미는 끝점과의 거리를 재서 얼마나 더 잡아먹을지)
그리고, solution 함수에서 답을 찾는 결정적인 트리거가 된다. 한 번 튕긴 개미를 그다음 튕길 땐 투명인간 취급한 것
투명인간 취급하지 않는다는 것을 구현하려면 '한 번 움직일 때마다 모든 개미들의 위치를 바꿔야 되지 않을까?', '그럼 시간 복잡도는?' 그 외에도 고려해야 할 것들이 엄청 많아졌다. 그래서 '아 이건 아니구나' 뼈저리게 느꼈다.
#include <iostream>
#include <vector>
using namespace std;
// 최솟값을 구하는 것과 반대로 최댓값을 구하는 것은 반으로 나누었을 때
// 중간을 기준으로 왼쪽은 다 오른쪽 방향, 오른쪽은 다 왼쪽 방향
// 으로 갔을 때 최댓값이 구해지는 거 같다.
// 확실하지 않아서 노트에 이 경우와 다른 찝찝한 경우를 구현해봤지만
// 이 경우가 더 높은 시간을 가졌다.
// >>
// 2 6 7의 경우, 최댓값을 구할 때 지금 생각한 솔루션이 8이지만
// 최댓값이 나올 거 같은 다른 경우도 8이었다.
// 홀수일 때만 이런 건가
// 어떻게 구현해야 할까
// 지금 현재 걸리적거리는 부분 >> 사이즈가 홀수일 때는?
int solution(vector<int>& ants, int halfIdx, bool Direction) { // 시간 구하기
// halfIdx를 기준으로 왼쪽은 오른쪽으로 오게 하고, 오른쪽은 왼쪽으로 오게 한다.
// 아 잠만
// 아.. 아... 논리 잘못 잡았ㄷ 아...
}
int maxTime(vector<int>& ants, int length) { // Call-By-Reference로 시간 줄임
int halfIdx; // 시간을 재는 개미 (시작이 되는 위치)
if (ants.size() % 2 == 1) { // 개미의 개수가 홀수일 때
halfIdx = ants.size() / 2;
}
else { // 짝수일 때
int a = (ants.size() / 2) - 1;
int b = ants.size();
int aIdx = ants[a];
int bIdx = length - ants[b];
if (aIdx >= bIdx) { // a와 b가 같은 경우는 둘 중 무엇이 되도 상관 없다
halfIdx = aIdx;
}
else {
halfIdx = bIdx;
}
}
bool Direction = 1; // 1일 때 오른쪽, 0일 때 왼쪽
if (ants[halfIdx] - ants[halfIdx - 1] > ants[halfIdx + 1] - ants[halfIdx]) { // right 먼저 부딪히기
Direction = 1;
}
else {
Direction = 0;
}
return solution(ants, halfIdx, Direction);
}
int main() {
int T;
cin >> T;
for (int i = 0; i < T; i++) {
int length, n;
cin >> length >> n;
int half = length / 2;
int minValue = 0;
vector<int> ants; // 개미 위치 배열
for (int j = 0; j < n; j++) {
int idx;
cin >> idx;
int value;
if (idx <= half) {
value = idx;
}
else {
value = length - idx;
}
// 차후에 디버깅할 때 이런 식으로 오류를 찾는 것도 도움이 될 거 같아 주석으로 남겨둠
// 특정한 값이 이상하게 나온다 >> 특정한 값이 나온다면 그 때의 입력 값 혹은 관련된 값은 무엇인지를
// 파악하기 위한 디버깅이었다 생각한다.
/*
if (value == 100) {
cout << "check: " << idx << '\n';
}
*/
if (value > minValue) {
minValue = value;
}
ants.push_back(idx);
}
// 가장 빠른 시간은 막대의 길이를 반으로 나누었을 때
// 중간을 기준으로 왼쪽은 다 왼쪽 방향, 오른쪽은 다 오른쪽 방향
// 으로 갔을 때 제일 늦게 떨어지는 개미의 시간이 최소 시간이다.
cout << "min: " << minValue;
// 최댓값까지 구하려니 main이 꽤나 길어진다. >> 함수 선언
cout << ", max: " << maxTime(ants, length);
cout << '\n';
}
}사진도...



'PS > BOJ' 카테고리의 다른 글
| [알고리즘] 백준 6064번 카잉 달력 (C++), 정수론..? (0) | 2021.10.28 |
|---|---|
| [알고리즘] 백준 17266번: 어두운 굴다리 (C++), 아이디어 능력이 더 좋아지면 좋겠다 (0) | 2021.10.27 |
| [알고리즘] 백준 17626번: Four Squares (C++), 오래간만에 DP 포스팅 (0) | 2021.10.25 |
| [알고리즘] 백준 1074번: Z (C++), 단순한 재귀가 아닌 분할 정복 (0) | 2021.10.23 |
| [알고리즘] 백준 2630번: 색종이 만들기 (C++), 분할 정복 드디어 (0) | 2021.10.23 |




