| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 백트래킹
- 세그먼트 트리
- c++
- NEXT
- lazy propagation
- Overfitting
- object detection
- 다익스트라
- 이분 탐색
- 크루스칼
- 조합론
- 분할 정복
- 우선 순위 큐
- 너비 우선 탐색
- 미래는_현재와_과거로
- 알고리즘
- pytorch
- 플로이드 와샬
- 가끔은 말로
- 가끔은_말로
- 자바스크립트
- dropout
- 문자열
- back propagation
- tensorflow
- 회고록
- DP
- dfs
- BFS
- 2023
- Today
- Total
Doby's Lab
왜 U-Net의 Output에서는 ReLU가 아니라 Sigmoid를 쓸까? 본문
🤔 Problem
세션을 진행하던 중 논문 리뷰에 대해 피드백을 진행하다가 질문을 받았다. '모델 내에서는 ReLU를 쓰는데 왜 마지막에서는 갑자기 Sigmoid'를 쓰나요?', 솔직하게 당황했다.
결론적으로, 간단히 말하면 이 질문에 대한 답은 확률로 간단하게 표현하기 위함이라 정리할 수 있다.
이에 대해서 'ReLU에 비해 상대적으로 Sigmoid의 Output이 기준 값 0.5에 의하여 0과 1로 판별하기 쉽다.(?)'라고 답한 거 같다. 사실 정확하게 기억이 안 난다. 암튼 틀린 답이었다. Sigmoid의 출력을 0 혹은 1로 가진다고 했었나? 그랬다면, 왜 그런 말을 했을까...
그리고, 나 스스로도 답이 시원찮아서 '모델 내에서 Sigmoid를 쓰지 않는 이유'라는 반대의 경우에서도 설명했다. 이는 Sigmoid의 미분 최댓값이 0.25이기 때문에 모델의 깊으면 깊을수록 역전파 시에 Gradient Vanishing 문제가 발생할 확률을 높이기 때문이라 설명했다.
그래서, 세션이 끝나고도 찝찝해서 이에 대해 생각해 보고, 정답이 아닌 나의 생각을 적어본다.
왜 Semantic Segmentation(U-Net)의 Output에서는 ReLU가 아니라 Sigmoid를 쓸까?
(다 쓰고 나서 생각해 보니 이건 Binary Classification이라 생각해도 될 문제였다.)
+ 추가적으로, 이에 대해서 다이브의 다른 분야 멘토님들과 의견을 나누어보았다. 다들 늦은 밤인데도 너무 감사하게 다양한 관점에서 의견을 얘기해 주셔서 이 글에 멘토님들의 의견을 더 적어둔다. 감사합니다 멘토님들 :)
1️⃣ 기준 값에 대한 범위의 문제
2개의 생각이 떠올랐는데, 1번째 생각은 ReLU가 가지는 범위를 생각했다. ReLU가 가질 수 있는 값의 범위는 \([0, \infty)\)와 같다. \(\infty\) 값이 터무니없이 너무 크기 때문에, 최종 활성화 함수로 ReLU를 가지는 모델이 학습을 했다는 상황과 그 모델에 입력 샘플을 줬을 때 상황을 가정해 보자.

그때 출력 Mask에서 픽셀의 최솟값이 0이고, 최댓값이 1.2라고 해보자. 그러면, 해당 출력 Mask에서 Positive와 Negative를 가를 수 있는 기준 값은 무엇이 되어야 하는가? 0.6이 되어야 하는가?
0.6이 된다고 했을 때, 다른 샘플을 줬더니 출력 Mask에서 1.4가 나온다면, 다시 기준 값은 0.7로 바꿔야 하는가?
물론, 출력이 1에 가깝게 학습을 하기 때문에 일반적으로 Sigmoid에서 0.5를 기준 값으로 써서 Positive와 Negative를 가르듯이 ReLU도 0.5를 쓴다고 해도 큰 문제는 없을 것으로 예상한다.
하지만, 이것은 Sigmoid와 비교했을 때는 문제점이라는 생각까지 든다.
그래서 ReLU 값이 가지는 범위에 대해 Positive와 Negative를 구분 지을 수 있는 기준 값을 정하는 것이 모호하다.
이 때문에 '\((0, 1)\)을 범위로 갖는 Sigmoid를 사용해서 보편적인 기준 값인 0.5를 사용하여, ReLU에 비해 안정적으로 Positive와 Negative를 구분할 수 있게 하는 것이 아닌가?'라는 것이 첫 번째 생각이다.
+ 이에 대해서 멘토님들의 의견은 이진 분류에서 나오는 출력 값을 클래스에 대한 '확률'로 사용하기 때문에 ReLU로 사용할 경우, \([0, \infty)\)의 범위를 다시 \((0, 1)\)로 표현하여 확률처럼 해석할 수 있도록 하는 번거로움이 생긴다. 결론적으로, 1번에 대해서는 다들 같은 생각이었습니다. '확률 값으로 표현'이라는 키워드로 접근을 했을 때, 타당성이 부여되는 듯했습니다.
2️⃣ Gradient Descent의 동등성 문제
+ 토의를 통해서 해당 가설은 문제가 될 수 없다는 해석이 되어서 폐기를 시켜야 하는 가설이지만, 접근을 하는 과정에서 흥미로웠다는 생각이 들어서 이를 그대로 남겨두고, 그 아래에서 왜 문제가 되지 않는 것인지에 대해 새로운 해석을 추가로 글을 남겨두었습니다.
위와 똑같이 ReLU를 최종 활성화 함수로 사용하는 모델이 있고, 이번에도 샘플을 넣었다.
이때, 어느 픽셀에서는 출력 값이 0.6이었고, 다른 픽셀에서는 출력 값이 0.8이었으며, 두 픽셀 모두 실제 값이 1이라고 가정하자.
그리고, 터무니없겠지만 모델을 \(Model = \sigma(Wx+b), \:(\sigma = \text{acti function})\)라고 가정해 보자. 두 출력 0.6과 0.8에 대해서 \(W\)를 업데이트하기 위해서 Gradient Descent를 한다고 하면, 식은 아래와 같이 나올 것이다. (손실 함수는 MSE Loss로 가정)
$$ \frac{\delta L}{\delta w} = \frac{\delta L}{\delta \sigma(z)} \cdot \frac{\delta\sigma(z)}{\delta z} \cdot \frac{\delta z}{\delta w} $$
미분의 원리에 따라 첫 번째 항은 모델의 출력에 의존한 값을 갖고, 세 번째 항은 모델의 입력에 의존한 값을 가지게 되는데 두 번째 항은 모델의 출력이 0.6이든, 0.8이든 관계없이 무조건 1을 갖게 된다. ReLU의 입력이 양수일 때 미분 값은 무조건 1이기 때문이다.
당연히 위 1번처럼 이것은 문제가 되지 않을 수도 있다. 이미 첫 번째 항과 세 번째 항에서 입출력에 의해 의존한 값을 업데이트할 값으로 알려주기 때문이다. 그래도 이게 맞을까?
Sigmoid라면, 이것이 문제가 될 거란 생각도 하지 않는다. 왜냐하면, 아래의 Sigmoid에 입력에 대한 미분 값을 시각화한 그림을 보면 이해가 된다. 혹은, 아래의 Sigmoid의 미분을 본다면, 이해가 된다.
$$ \Phi'(x) = \Phi(x)(1-\Phi(x)) $$
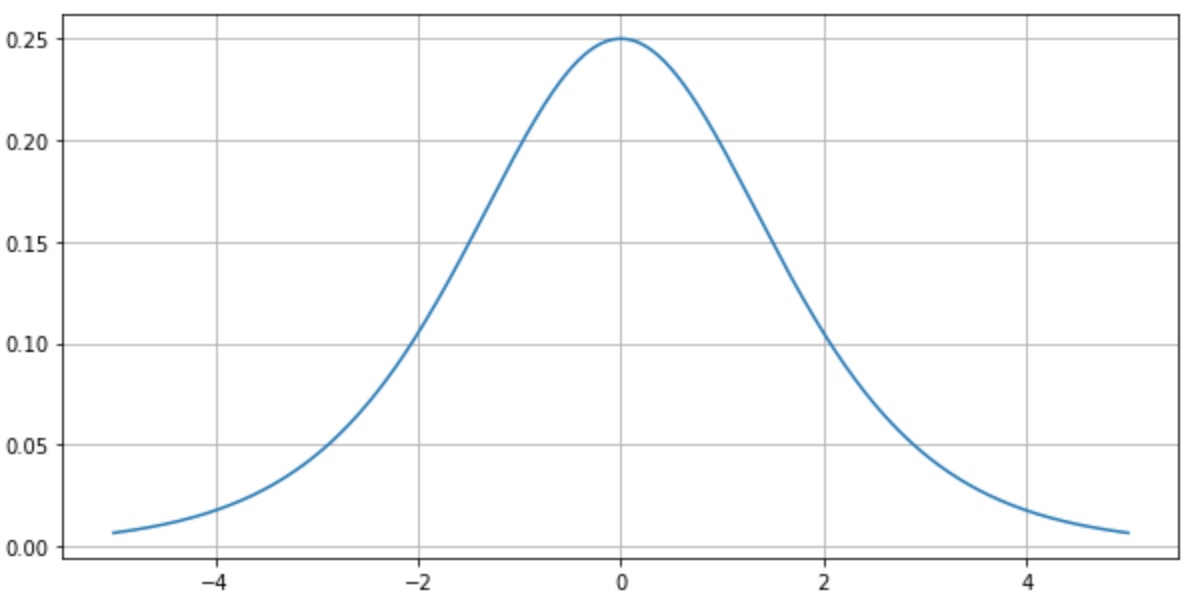
모델의 입출력이 같다면, Gradient Descent의 첫 번째 항, 세 번째 항은 ReLU를 쓰든, Sigmoid를 쓰든 활성화 함수에 의존하지 않아서 같기 때문에 고려하지 않고, 두 번째 항을 단독으로 봤을 때, 모델의 출력에 따른 미분 값이 달라진다.
모델의 출력이 0.6이었다면, 1에 더 가까워지기 위해 \(\frac{\delta\sigma}{\delta z}\) 값이 0.8일 때보다 큰 값을 가지게 된다.
다시 말해서 \(\frac{\delta\sigma}{\delta z}\)의 값이 ReLU일 때는 출력이 달라도 변하지 않는데, Sigmoid일 때는 변하는 값을 갖기 때문이라 볼 수 있다. 서로 다른 출력에 대해서 업데이트해야 하는 양이 같으면 안 되기 때문이다. (다시 말하지만, 다르긴 하다. 하지만, Gradient Descent의 두 번째 항에 대해서만 얘기를 해보는 것이다.)
즉, 최종 Output에서는 ReLU가 아닌 Sigmoid를 사용해야 모델을 최적화하는 과정에서 더 정교한 Gradient 값을 가질 수 있게 된다.
+ 사실 이미 ReLU가 아닌 Sigmoid를 쓰는 이유는 '확률 값으로 표현하기 위함'에서 끝이 났다. 하지만, 2번에 대해서 멘토님들과 이야기를 해봤을 때, 내 의견에 반론을 할 수 있는 새로운 생각이 들어서 이를 남겨둔다.
Gradient Descent를 구하는 식 \(\frac{\delta L}{\delta w}\) 는 미분의 연쇄 법칙에 의해서 여러 항들로 풀어쓸 수 있다. 즉, 독립적으로 항들을 식을 간단화하여 볼 수는 있다. 그런데, 독립적으로 다루어 볼 수도 있을까? 아니다. 합성함수의 미분법에 따르면, 이는 무조건 곱해져 있는 형태이고, 따로 분리를 할 수 없기 때문에 연쇄 법칙으로 풀어쓴 각 항들에 대해서 독립적인 해석은 불가능하며, 무조건 전체적인 항들의 곱으로 해석을 해야 한다.
즉, 위에서 말한 2번째 항이 ReLU를 사용했을 때는 어떤 입출력이건 같지 않느냐?(양수라는 조건 하에)라는 의문에 대해서 1번째 항과 3번째 항이 입출력에 의존하여 결과에 서로 다른 영향을 미치고 있고, 이를 해석할 때는 모두 하나의 항처럼 해석을 해야 하기 때문에 Gradient Descent의 동등성과 정교함이라는 문제를 언급하기에는 다소 부적절함이 있을 거라는 것이 새로운 의견이자 반론이다.
😀 P.S.
이 문제가 결국 Binary Classifcation일 때도 같은 문제라고 볼 수 있다.
그리고, 이 문제에 대해서 생각하면서 정답이 정해져 있는 문제는 아닐 수도 있겠다는 생각이 들기도 했다.
+ 이에 대해서 내가 의문을 품었던 점들 이외에도 새롭게 알게 되는 것들이 정말 많았다.
은닉층에서 Sigmoid가 아닌 ReLU를 사용하는 이유는 Gradient Vanishing 문제를 해결하는 것도 맞지만, 음수인 출력을 모두 버리는 ReLU를 왜 사용하냐는 관점에 대해서는 출력을 Sparse 하게 만들어서 연산의 효율성이 올라간다는 의견이 있었다.
https://www.quora.com/Should-ReLU-be-avoided-for-input-data-that-has-a-lot-of-negative-values-in-machine-learning-models-as-an-activation-function-given-that-ReLU-totally-disregards-negative-values-by-returning-a-zero-output
Should ReLU be avoided for input data that has a lot of negative values in machine learning models as an activation function, gi
Answer: ReLU activations shouldn’t be avoided just because the input features are negative. The features are multiplied with weights that can be negative as well, thus making the actual inputs to the neuron positive. If you consider the topology of a sin
www.quora.com
또한, 요즘은 ReLU가 아닌 GELU를 많이 사용한다고 한다. 최근에 ConvNext를 리뷰하면서 저 함수를 많이 봤던 거 같은데, 단순히 시각화된 것만 봤을 때는 모든 점에 미분이 가능한 것처럼 보여서 쓰는 건가?라는 의문이 들기도 했었다. 이에 대해서는 추후에 '왜 GELU로 대체되고 있을까?'라는 이유로 생각을 해봐야겠다.
마지막으로, 내가 틀렸던 문제는 Sigmoid가 0.5를 기준으로 0과 1을 분류한다고 설명했던 것이라 하셨다. 0.5라는 임곗값은 Sigmoid와 연관이 없다는 것이 그에 대한 답변이었다.
그래서, 이 부분에 대해 0과 1로 분류하는 임곗값을 구하는 건 ROC Curve를 그려서 임곗값을 구한 다음에 분류하는 것이 맞고, 일반적으로 0.5를 많이 쓰는 것은 설명에 있어 조금 더 쉬운 관점을 제안하거나 결국에 저자 마음이라고 하신다.
아직도 배울 게 많다. 다시 한번, 늦은 시간에 멋진 의견들을 말해준 멘토님들께 감사드립니다..:)
'Daily > temp.txt (애매한 글들 모음)' 카테고리의 다른 글
| Git main branch에 올릴 때 참고 링크 모음 (0) | 2023.12.25 |
|---|---|
| PyTorch 기본 스터디 끝! (0) | 2023.11.21 |
| 의료 분야 AI 적용 사례 5가지 정리 (0) | 2023.07.18 |
| 체계적인 프로젝트를 위한 WandB (1) - 기록하기, 기초 (0) | 2023.07.12 |

