| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- 회고록
- 미래는_현재와_과거로
- 플로이드 와샬
- 백트래킹
- 다익스트라
- tensorflow
- 문자열
- dropout
- 우선 순위 큐
- 크루스칼
- 알고리즘
- Overfitting
- 조합론
- 이분 탐색
- c++
- 가끔은 말로
- back propagation
- object detection
- DP
- 세그먼트 트리
- 자바스크립트
- 가끔은_말로
- dfs
- 분할 정복
- 너비 우선 탐색
- lazy propagation
- BFS
- NEXT
- 2023
- pytorch
- Today
- Total
Doby's Lab
Kaggle - Learn Feature Engineering : Clustering With K-Means 본문
Kaggle - Learn Feature Engineering : Clustering With K-Means
도비(Doby) 2022. 10. 17. 23:09[이 글은 Kaggle의 Learn을 토대로 작성되었습니다. 문제가 될 시 삭제 조치하겠습니다.]
(오역되어 잘못 설명된 부분이 있을 수 있습니다.)
https://www.kaggle.com/code/ryanholbrook/clustering-with-k-means
Clustering With K-Means
Explore and run machine learning code with Kaggle Notebooks | Using data from FE Course Data
www.kaggle.com
Category
- Introduction
- Clusters Labels as a Feature
- K-Means Clustering
- Example - California Housing
Introduction
이번엔 Unsupervised Learning Algorithm을 이용해봅니다. 이 알고리즘은 target이 필요하진 않고, feature의 구조를 표현하기 위해 데이터로부터 어떤 정보를 가져옵니다. Feature Engineering이라는 문맥에서 Unsupervised Algorithm을 'Feature Discovery' 기술로 생각할 수 있습니다.
Clustering은 데이터 간의 유사성을 기반에 두고 데이터들을 각 그룹에 그룹화시키는 것을 의미합니다. Clustering을 말하기를 '유유상종'이라 볼 수 있습니다.
Clustering을 Feature Engineering으로 보고, Cluster Label을 사용함으로써 복잡한 관계성을 띄는 데이터들을 간단히 풀어나갈 수 있습니다.
Cluster Labels as a Feature
single real-valued feature에 clustering을 적용하면 'binning' 혹은 'discretization'같은 변환을 시켜 데이터 간의 구분을 짓습니다. multiple feature에 대해서는 'multiple-dimensional binning'(or vector quantization) 같은 변환을 시켜 구분을 짓는다고 보면 됩니다. 아래 그림이 그 예시입니다.

오른쪽 figure에 대해 DataFrame에 Cluster Label을 추가했다면, 아래와 같은 DataFrame이 만들어질 것입니다.
| Longitude | Latitude | Cluster |
| -93.619 | 42.054 | 3 |
| -93.619 | 42.053 | 3 |
| -93.638 | 42.060 | 1 |
| -93.602 | 41.988 | 0 |
'Cluster' feature가 Categorical Feature임을 기억하는 것은 꽤 중요합니다. 아래 figure는 Clustering Algorithm을 통해 만들어진 Label Encoding을 보여줍니다. Model에 따라서 One-hot Encoding이 더 적합할 수 있습니다.
Cluster Label을 추가함에 있어서 영감을 받아 복잡한 관계를 하나의 간단한 feature로 만들어버릴 수 있습니다. Model은 한 번에 복잡한 관계에 대해서 배우는 것보다 Cluster Label을 학습함으로써 더 간단해질 수 있습니다. 이것을 '분할 정복' 전략이라 합니다.
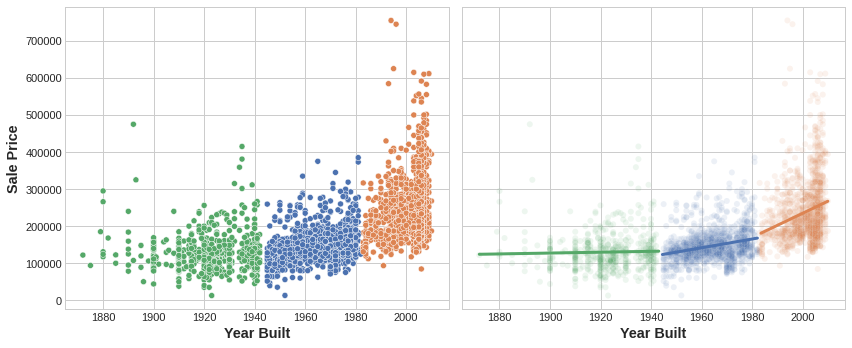
왼쪽 figure는 복잡한 관계에 대해 학습한 모델을 보여주고, 오른쪽 figure는 Cluster Label을 학습한 것을 보여줌으로써 Clustering이 어떻게 간단한 Linear Model로 개선시키는지 보여줍니다.
K-Means Clustering
수많은 Clustering Algorithm이 있지만 각 Algorithm들이 'Similiarity' 혹은 'Proximity'를 어떻게 측정하냐에 따라 다릅니다. 이번엔 직관적이고 Feature Engineering에 적용하기 쉬운 K-Means에 대해 알아봅시다. (어떤 상황에 따라서 적합한 Clustering Algorithm들이 있습니다.)
K-Means Clustering은 Euclidean Distance를 사용하여 실질적인 거리를 사용하여 측정합니다. Centroid라 불리는 점 여러 개를 feature-space에 배치함으로써 Cluster를 생성합니다. Dataset의 각 점들은 가장 가까운 Centroid가 어디인지에 따라 Cluster에 할당됩니다. K-Means에서 K는 Centroid를 뜻하며, 사용자가 정할 수 있는 Hyperparameter이기도 합니다.
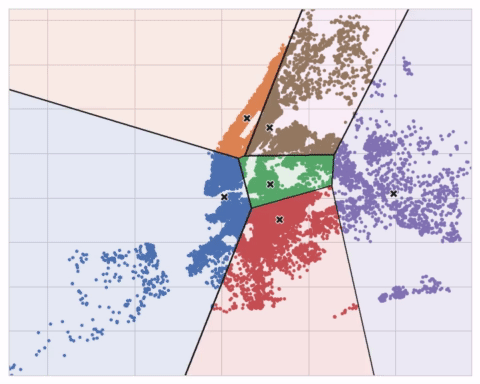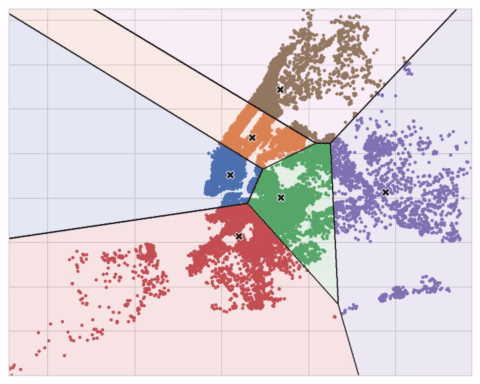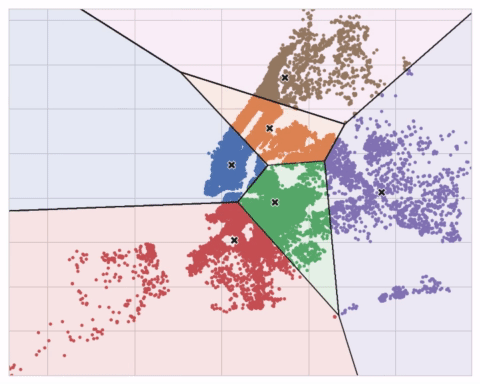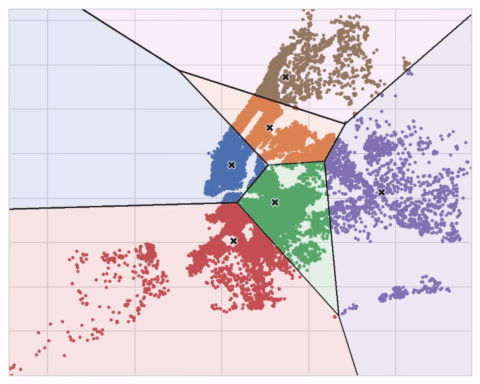
Centroid는 점점 퍼져가는 원을 형성하며 다른 Centroid가 만든 원이 겹쳐지면 선을 형성하는데 그렇게 만들어진 그림을 'Voronoi tessallation'이라 합니다. 이 tessallation은 다음 데이터가 어떤 Cluster에 할당될 것인지 보여주고, 이러한 tessallation은 training data로부터 만들어집니다.
'Ames dataset'의 K-Means Clustering figure를 봅시다. 아래에는 Voronoi Tessallation과 Centroid가 있습니다.
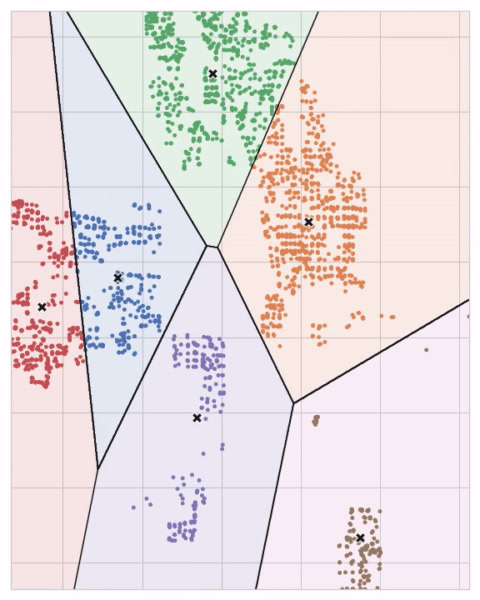
Scikit-Learn에서 구현된 K-Means 알고리즘의 3가지 Parameter(n_clusters, max_iter, n_init)을 사용해보면서 K-Means의 작동 원리를 알아봅시다.
처음엔 n_clusters(centroid의 개수)만큼 랜덤한 숫자들을 생성합니다. 그리고, 아래와 같은 2가지 과정이 반복됩니다.
- 점들을 가장 가까운 Centroid에 할당한다.
- Centroid를 할당된 점들 사이의 거리를 최소화하기 위해 이동시킨다.
이것을 Centroid들이 더 이상 움직이지 않을 때까지 반복하거나, max_iter로 지정된 최대 반복 횟수만큼 반복합니다.
종종 랜덤하게 생성된 Centroid들은 Clustering이 잘 되지 않기 때문에 n_init을 통해 지정된 횟수만큼 Algorithm을 반복합니다. 반복된 과정 중에서 Centroid로부터 각 점들의 거리가 제일 최소화된 Clustering을 리턴합니다.
아래 애니메이션은 알고리즘의 동작 과정을 보여줍니다. 이 애니메이션은 초기의 Centroid에 대한 의존성과 수렴할 때까지의 반복의 중요성을 보여줍니다.
Cluster의 개수가 많을 때는 max_iter를 증가시키고, 복잡한 데이터셋에 대해서는 n_init을 증가시키는 게 좋습니다. 평상시에는 Centroid의 개수(n_clusters)만 조정하는 게 일반적입니다. 어떤 모델을 쓰는지, 예측하고 싶은 게 무엇인지에 따라 Centroid의 개수를 적합하게 조정해야 합니다. 그래서 교차 검증을 통해 어떤 Hyperparameter를 찾는 것도 좋은 방법입니다.
Example - California Housing
California Housing Dataset에서 'Latitude'와 'Longitude' feature를 사용하고, 'MedInc'(Median Income)이라는 feature까지 사용하여 Clustering 함으로써 경제적인 특징을 넣은 Cluster를 만들어봅시다.
K-Means Clustering은 Scale에 있어 예민하기 때문에 Normalization이나 Standardization같은 Scaling을 해주는 것이 좋습니다. 우리가 사용하려는 Feature들은 다 같은 Scale에 있기 때문에 그대로 내버려둡시다.
# Create cluster feature
kmeans = KMeans(n_clusters=6)
X["Cluster"] = kmeans.fit_predict(X)
X["Cluster"] = X["Cluster"].astype("category")
X.head()| MedInc | Latitude | Longitude | Cluster | |
| 0 | 8.3252 | 37.88 | -122.23 | 0 |
| 1 | 8.3014 | 37.86 | -122.22 | 0 |
| 2 | 7.2574 | 37.85 | -122.24 | 0 |
| 3 | 5.6431 | 37.85 | -122.25 | 0 |
| 4 | 3.8462 | 37.85 | -122.25 | 2 |
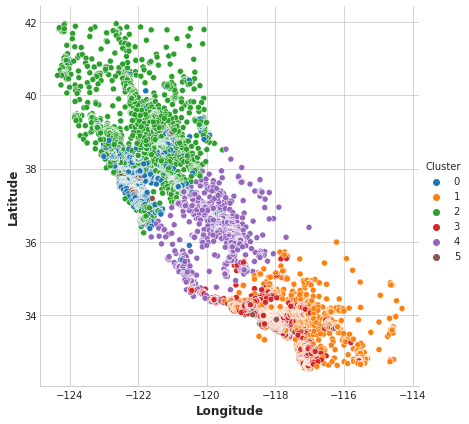
Cluster가 얼마나 효과가 있었는지 Couple Plot을 통해 시각화해봅시다. Scatter Plot을 통해 Cluster의 위치적인 분포를 봅시다. figure는 해안의 고소득 지역들에 대해 분할을 해놓은 것 같습니다.
이 Dataset에서 Target은 'MedHouseVal'(median house value)이며 Clustering의 정보가 유익하다면 'MedHouseVal'에 따라 분리가 잘 되어 있어야 합니다. 하지만, 실제로는 아래에 보이는 figure와 같습니다.
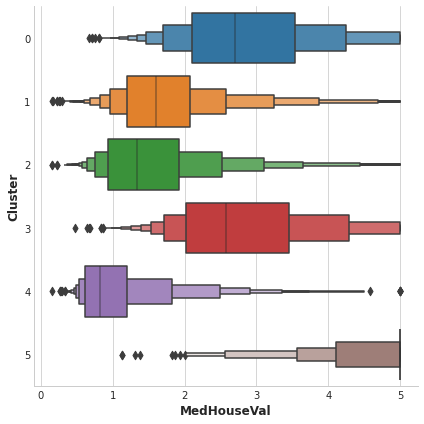
Clustering이라는 Unsupervised Algorithm을 통해 복잡한 관계를 지니는 데이터에 대해 간단한 'Cluster Label'이라는 Feature를 만듬으로써 Complexity를 줄이고, 이러한 Cluster들이 시각화를 통해 Target과 분리성에 있어서 informative 한 지 알아보았습니다.
'Data Science > Feature Engineering' 카테고리의 다른 글
| Kaggle - Learn Feature Engineering : Target Encoding (0) | 2022.10.22 |
|---|---|
| Kaggle - Learn Feature Engineering : Principal Component Analysis (0) | 2022.10.22 |
| Kaggle - Learn Feature Engineering : Creating Features (0) | 2022.10.13 |
| Kaggle - Learn Feature Engineering : Mutual Information (0) | 2022.10.10 |




