| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- Overfitting
- 이분 탐색
- back propagation
- c++
- 미래는_현재와_과거로
- 조합론
- 크루스칼
- 플로이드 와샬
- dfs
- 2023
- 회고록
- 우선 순위 큐
- 다익스트라
- 너비 우선 탐색
- 가끔은_말로
- 문자열
- 자바스크립트
- object detection
- DP
- pytorch
- dropout
- 분할 정복
- NEXT
- 세그먼트 트리
- lazy propagation
- 백트래킹
- 가끔은 말로
- BFS
- 알고리즘
- tensorflow
- Today
- Total
Doby's Lab
[알고리즘] 최소 스패닝 트리 (C++), 크루스칼 알고리즘 본문
https://www.acmicpc.net/problem/1197
1197번: 최소 스패닝 트리
첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이
www.acmicpc.net
공부한 블로그
(https://ansohxxn.github.io/algorithm/mst/)
(https://yabmoons.tistory.com/186)
[개요]
최소 스패닝 트리란?
- 방향이 없다. (양방향)
- 사이클이 없다. >> 트리라고 부르는 이유
- 모든 노드가 연결되어 있다. (간선이 없는 노드가 존재하면 안 된다.)
- 트리의 모든 가중치의 합이 최솟값이어야 한다.
방향이 없다는 점에서 DAG(Directed Acyclic Graph)와도 비교할 수 있다.
2번의 경우는 (https://ko.gadget-info.com/difference-between-tree) 다음 글을 참고하면 알 수 있다.
즉, 모든 노드를 연결하는 트리인데 트리의 모든 가중치의 합이 최소가 되는 트리를 최소 스패닝 트리 (Minimun Spanning Tree)라고 한다.
그림으로 보자.
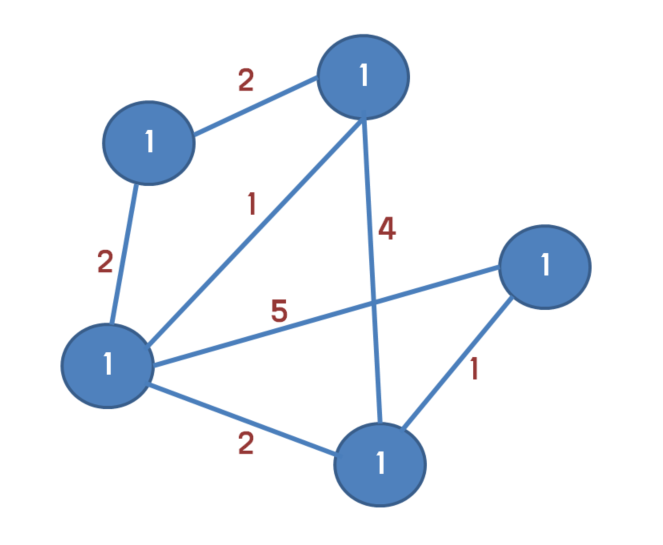
다음과 같은 양방향 가중치 그래프가 있다.
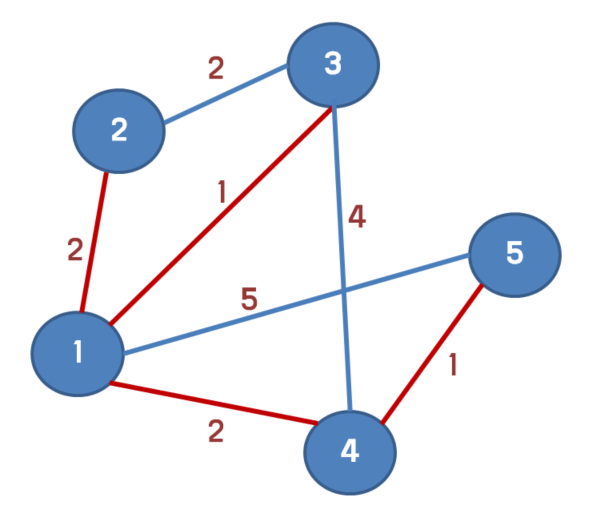
그럴 경우 최소 스패닝 트리를 구하면 빨간색 간선들이 선택된다.
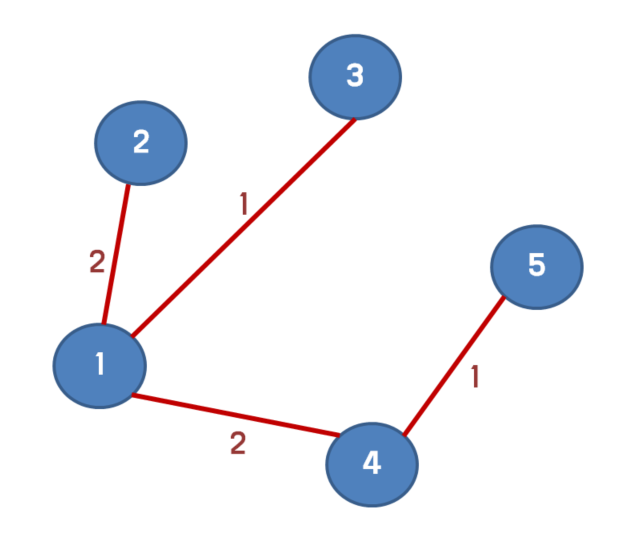
모든 노드로 갈 수 있는 최소 스패닝 트리가 완성되었다.
개념적인 부분에서 최단 경로 알고리즘과 살짝 헷갈릴 수 있는 부분이
최단 경로 알고리즘은 어느 노드에서 어느 노드로 갈 때 최소 가중치이고,
최소 스패닝 트리는 트리 구조를 가지며 모든 간선의 가중치의 합이 최솟값으로 만들어지도록 하는 것이다.
[구현]
사이클의 형성을 막기 위해 다음 방법을 쓴다.
각 노드의 부모 노드(루트)를 구한다. 부모 노드가 되는 조건은 연결되어있는 노드들 중 가장 작은 번호를 가지는 값이다.
간선을 추가할 때 간선이 연결된 두 정점의 부모 노드가 같은 경우 이 간선은 추가하지 않는다.
<구현 순서>
- 각 노드의 부모는 자기 자신으로 초기화한다.
- 간선의 가중치를 오름차순으로 정렬한다.
- 간선을 for문을 통해 돈다.
- 두 정점 간의 부모 노드를 확인(find)한다.
- 부모 노드가 다를 경우 두 정점을 합친다.(Union)
<시간 복잡도>
크루스칼 알고리즘의 구성 중 정렬 알고리즘에 제일 시간을 의존하기 때문에
>> O(ElogE), E = 간선의 개수
최소 스패닝 알고리즘 중에 프림 알고리즘(우선순위 큐 사용)은 (ElogV + VlogV)로
간선이 적은 Sparse Graph의 경우 크루스칼 알고리즘이 유리하고,
간선이 많은 Dense Graph의 경우 프림 알고리즘이 유리하다.
// Spanning Tree
// 방향이 없고, 모든 노드를 포함하며, 사이클이 없는 형태
// 이 스패닝 트리에서 가중치의 합을 최소로 만드는 것을 최소 스패닝 트리라고 한다.
#include <iostream>
#include <vector>
#include <algorithm>
#define pii pair<int, int>
#define MAX (10000 + 1)
#define ll long long
using namespace std;
vector<pair<pii, ll>> edges;
int parent[MAX];
int v, e;
bool cmp(pair<pii, ll> a, pair<pii, ll> b) {
return a.second < b.second;
}
int getRoot(int node) {
// recursive call을 통해 부모 노드를 찾아간다.
if (parent[node] == node) {
return node;
}
return parent[node] = getRoot(parent[node]);
}
void unionParent(int a, int b) {
// 연결하는 방법: 두 노드의 루트 노드를 같게 한다.
int aRoot = getRoot(a);
int bRoot = getRoot(b);
if (aRoot < bRoot) {
parent[bRoot] = aRoot;
}
else {
parent[aRoot] = bRoot;
}
}
bool find(int a, int b) {
// 노드가 향하는 부모노드(루트 노드)가 같을 경우
// true를 리턴하여 둘이 연결할 경우 사이클이 발생한다고 알린다.
// 부모가 같지 루트가 같지 않은 경우 false를 리턴하여 연결해도 된다고 알린다.
int aRoot = getRoot(a);
int bRoot = getRoot(b);
if (aRoot == bRoot) {
return true;
}
else return false;
}
int main() {
cin >> v >> e;
for (int i = 0; i < e; i++) {
int a, b, w;
cin >> a >> b >> w;
edges.push_back({ {a, b}, w });
}
// 최소 스패닝 트리라서 간선 가중치가 작은 거부터 선택할 수 있도록 정렬
sort(edges.begin(), edges.end(), cmp);
// init 자기 자신의 부모를 자기 자신으로 초기화
for (int i = 1; i <= v; i++) {
parent[i] = i;
}
int answer = 0;
for (int i = 0; i < edges.size(); i++) {
if (!find(edges[i].first.first, edges[i].first.second)) {
unionParent(edges[i].first.first, edges[i].first.second);
answer += edges[i].second; // 가중치
}
}
cout << answer;
return 0;
}
'PS > Study Note' 카테고리의 다른 글
| SCC 알고리즘 2가지 (0) | 2022.04.02 |
|---|---|
| [알고리즘] Merge Sort (합병 정렬) 구현 (C++) (0) | 2022.03.01 |
| [자료구조] 우선순위 큐, 비교 연산자 (C++) (0) | 2021.11.30 |
| [알고리즘] 2차원 배열이란 키워드 (0) | 2021.11.24 |
| 최근 유용하게 쓰는 함수들 C++로 구현해놓은 거 (0) | 2021.11.09 |
